语音特征参数MFCC的提取过程是确保语音识别准确的关键步骤。 MFCC全称Mel-scaleFrequency Cepstral Coefficients，中文名叫梅尔倒谱系数。 是在Mel标度频率域提取出来的倒谱参数，Mel标度描述了人耳频率的非线性特性，它与频率的关系可用下式近似表示：

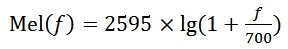
式中f为频率，单位为Hz。下图展示了Mel频率与线性频率的关系：

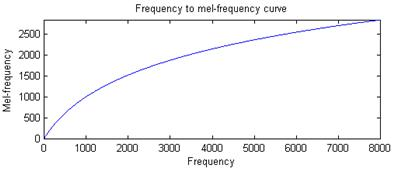
根据人耳听觉机理的研究发现，人耳对不同频率的声波有不同的听觉敏感度。从300Hz到3400Hz的语音信号对语音的清晰度影响最大。

一、预加重（Preemphasis）

预加重是MFCC特征提取的第一步，因为低频信号比高频信号具有更多的能量。这种跨越频率的能量下降(称为频谱倾斜)是由声门脉冲的性质引起的。提高高频能量使这些高共振峰的信息更容易被声学模型利用，提高了检测精度。

预加重是使用滤波器完成的，即先过滤出高频的声段，再进行加重操作，滤波器如下所示：

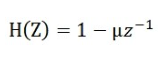
式中的值介于0.9-1.0之间，我们通常取0.97。

二、加窗（Windowing）

语音特征其实有很大的变化，我们在不同的情绪以及不同的环境中所收集的所谓频谱特征（spectral features）是不同的，所以我们认为语音其实是一个非平稳信号，这意味着他的统计特性在时间上不是恒定的。但我们一般认为在短时间内提取的频谱特征是平稳的。

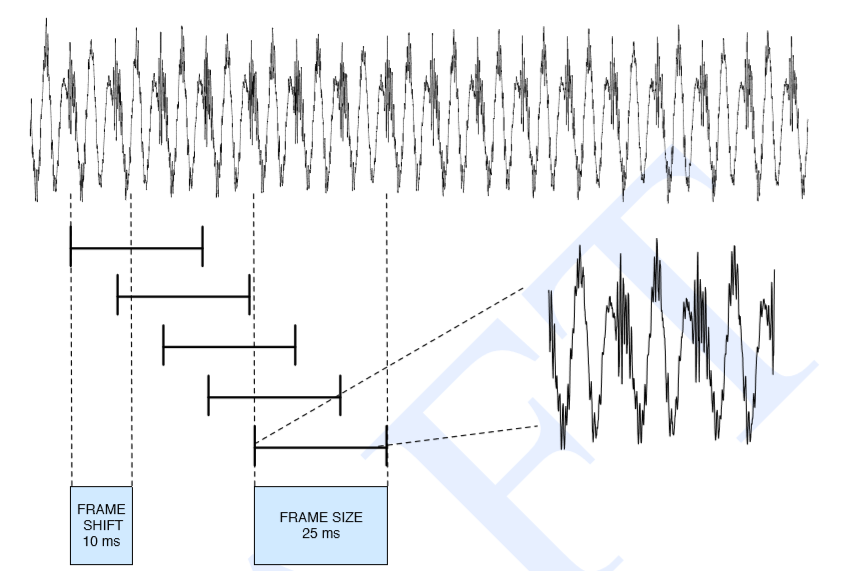
我们通过在某区域内使用窗口来提取波形，同时使用窗口的宽度 wide（以毫秒为单位）、连续窗口之间的偏移量 offset 以及窗口的形状 shape 来描述窗口过程，窗口提取到的语音称为帧，其中帧的毫秒值称为帧的大小 frame size （一般为25ms），并将连续窗口的左边缘间隔的毫秒值称之为帧的移动 （一般为10ms）frame shift。方程为：

y[n] = w[n]s[n]

其中n表示时间，s[n]表示语音原本的状态，w[n]表示窗口形状的处理，y[n]表示最终状态。

窗口形状的概念听起来比较抽象，以下例子将做一个说明。 上图中窗口提取出来的信号与原始信号一样，所以这些窗口都是矩形窗口，也是最简单的窗口。然而，矩形窗口可能会引起问题，因为它是垂直的，会在其边界处突然切断信号。当我们做傅里叶分析时，这些不连续点会产生问题。因此，在MFCC提取中使用的一个更常见的窗口是汉明窗口（Hamming Window），它将信号的值在窗口边界处缩小到汉明零，以避免不连续。方程如下(假设窗口为L帧长):

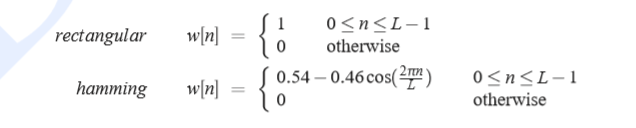
以下是一般情况的汉明窗，不同的a值会产生不同的汉明窗，一般情况下a取0.46。

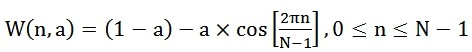
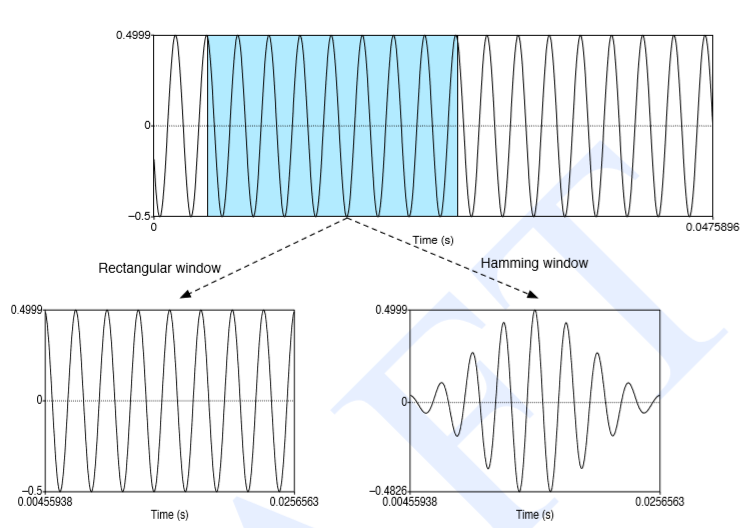
汉明窗得到的信号：

离散傅里叶变换（Discrete Fourier Transform）

乍一听到傅里叶变换感觉熟悉又陌生，这里先来简单复习一下。 傅里叶变换，表示能将 满足一定条件的 某个函数 表示成三角函数（正弦和/或余弦函数） 或者它们的 积分的线性组合。

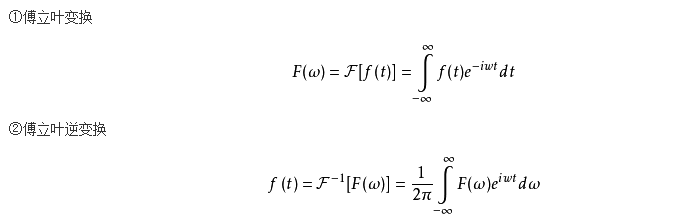
而离散傅里叶变换（DFT）是傅里叶变换在时域和频域上都呈离散的形式，在这里我们把一个个窗体作为输入，输出是一个个复数，表示信号中的频率分量的大小和相位， 计算过程比较复杂，但我们通常使用欧拉公式帮助我们分析：

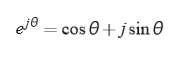
DFT定义如下：

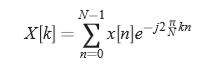
计算DFT的一种常用算法是快速傅里叶变换(FFT)，用于实现DFT十分有效，但只适用于FFF的N值是2的幂。

倒谱（The Cepstrum）

这里有一个有趣的文字游戏，频谱的前四个字母倒过来就是倒谱：

频谱 spectrum

倒谱 cepstrum

因为梅尔谱（Mel spectrum）来做特征提取会存在一定问题，为了解决这一点，我们下一步将进行倒谱（cepstrum）计算。

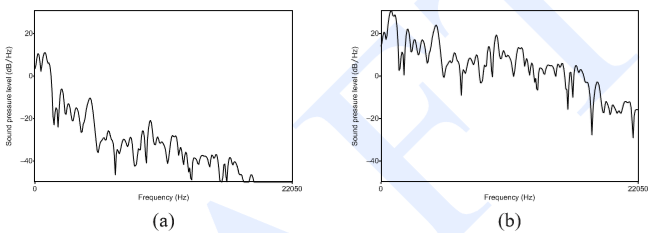
倒谱可以理解为频谱取log的频谱(spectrum of the log of the spectrum)，这句话我读的时候感觉不是人话，图形画出来大致是这样的：

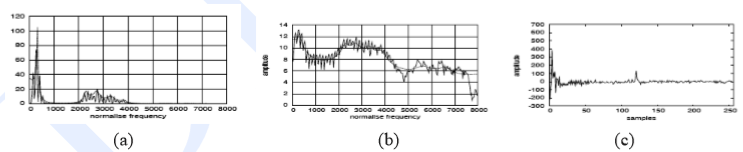
其中（a）是频谱的样子，(b)是频谱取log的样子，（c）是倒谱的样子。

倒谱系数具有一个非常有用的性质，不同系数的变量是趋于不相关的，而在频谱中不是这样的，这意味着高斯混合模型GMM不必表示所有MFCC特征之间的协方差，减少了参数的数量。对于一个有窗口的语音帧x[n]，经过如下的步骤成倒谱：

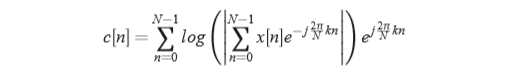
对于MFCC的提取，我们通常只取前12个值。

能量（Deltas and Energy）

每帧得到12个倒谱系数后，能量是第13个特征。对于时间样本t1到时间样本t2窗口内的信号x，能量为:

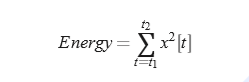
因为帧（frame）与帧之间不是恒定的，我们还需要添加与倒谱特性随时间变化的相关特性给13个特征（12个倒谱系数+能量），这个特性称 delta 或速度、double delta 或加速度。

我理解13个delta特征为：帧与帧之间的变化。

我们理解13个double delta特征为：帧之间的变化的变化（类似于加速度，描述速度的变化）。

算delta最简单的方法：

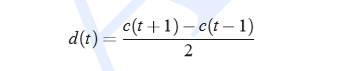
MFCC

添加能量后，39个MFCC特征就齐了：

 12 个倒谱系数
 12 个倒谱系数变化速率
 12 个倒谱系数变化速率的速率
 1  个能量系数
 1  个变化速率的能量系数
 1  个变化速率的速率的能量系数
 ————————————————————————————————
 39 MFCC 特征

同样，关于MFCC特征最有用的事实之一是倒谱系数往往是不相关的，这将使我们的声学模型更简单。