数据结构和算法是程序员的基本功,也是各大学校各大厂十分看重的敲门砖,本人参与过一些竞赛,竞赛除了考察对数据结构的掌握其实还存在许多的套路,这里进行一个总结与归纳,希望可以在日后参加竞赛时去得更好的成绩。
常见问题知识储备
最大值表示
最大值比较大不好表示的时候可以使用INT_MAX表示。
头文件
#include <limits.h>
指针基础
指针:
//获取变量的地址 &
int a = 1;
printf("%d\n", &a);
//指针变量用来存放指针(或者可以理解为地址)
int *p;
int* p; //两种情况等价
//要明确的是,定义完指针变量后,指针变量是 p,而不是 *p
//因为 & 可以得到变量的地址,所以给指针的赋值就变成了:
int a;
int *p = & a;
//所以地址 &a 是赋值给了 p 而不是 *p
//得到地址里的东西,还是使用 * ,把 * 当作是开启房间门的钥匙
int a = 233;
int* p = &a;
printf("%d\n", *p);
//output:233
指针与数组:
//数组的名称也具有收地址的作用
int a[10];
a == &a[0];
//指针变量的加减法在数组中最为常用
a + i == &a[i];
//输入 与 输出
int a[10];
for(int i=0;i<10;i++)
scanf("%d",a+i); //之前用 & 原来是表示地址,现在已经是存储的地址了所以不用&
for(int i =0;i<10;i++)
printf("%d\n", *(a+i)); //输出值
C语言数组放在main函数里面和外面的区别
几个概念:
栈区:由操作系统自动分配释放,存放函数的参数值,局部变量的值;当不需要时系统会自动清除。
堆区:由new分配的内存块,不由编译器管,由应用程序控制(相当于程序员控制)。如果程序员没有释放掉,程序结束后,操作系统会自动回收。
数据区:也称全局区或者静态区,存放全局的东西类似全局变量。
代码区:存放执行代码的地方,类似if else,while,for这种语句。
在main函数里面的数组是开在栈区(stack),在函数外面的是开在数据区的。栈区的内存比较小,所以当数组非常大的时候,就会报错。假如把数组放在数据区就不会出现这个问题,因为数据区的内存很大。
#include <iostream>
using namespace std;
//main函数外为数据区,差不多是真实计算的内存大小
long long a[20190325];
int main(int argc, const char * argv[]) {
// insert code here...
//main函数内 为栈区 内存块比较小
a[1]=1;
a[2]=1;
a[3]=1;
for(long long i=4;i<=20190325;i++){
a[i]=(a[i-1]+a[i-2]+a[i-3])%10000;
}
cout<<a[20190324]<<endl;
return 0;
}
时间复杂度处略估计
首先估计O(n),例如时间复杂度为O(n),n的规模为1000,那运算就是10^3.
O(n^2),规模为1000,那运算就是10^6.
对于一般的OJ来说,1s所能承受的运算次数是10^7~10^8
C++题目开数组下标确定
绝大部分题目会给出数组的上限指标,但是当数组界限未给定时要自行运算一下,就比如2013年蓝桥省赛中大臣的旅费一题,其中没有给定要输入的n(表示城市数)的规模,我在自己的Xcode上演算无误后提交却一直出现运行错误的问题。
查阅资料后发现蓝桥杯最大栈空间为256MB,于是我进行了如下演算:
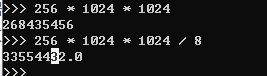
得出如下结论:最大可以开1乘10的7次方左右的数组空间
//合理开辟方法例子如下:
int a[10000000]; //二维数组最大合理大小
int a[1000][1000]; //二维数组最大合理大小
int形最大存储位数
int为4字节,也就是共32位存储,可以存储负数说明第一位用来存储符号,所以其表示范围为:
-2^31~2^31
2^31 = 2 147 483 648 (10位数)
ps : 值得注意的是,当两个int进行类似乘或者平方等位数增长类运算时,若突破10位后再用long long接收是接收不到正确的数字的,只能接收益处的数字,所以当面临溢出风险时最好在运算前直接设为long long型
这里给出所有数据类型:
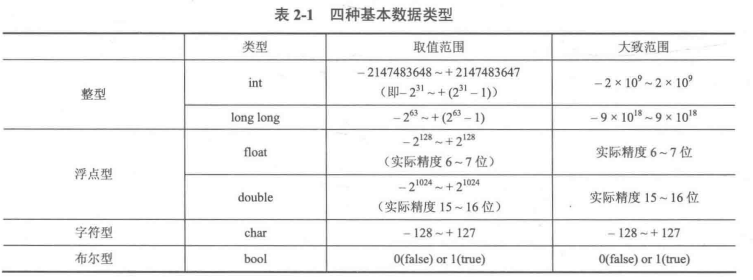
Excel日期计算
Excel可以帮助我们对日期直接进行加减天数的计算,但是只识别1900-1-1日之后的日期。
位运算
想成为高级程序员躲不开位运算。
+ - 需要 2 个CPU时钟
位预算 需要 1 个CPU时钟
* 需要 4 个CPU时钟
/ 需要 40 个CPU时钟
位运算会将数据显变换成二进制再进行演算:
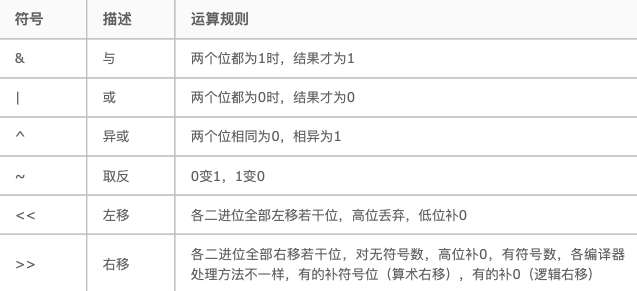
闰年判断
闰年的判断其实有两个条件:
1.年份能被4整除但是不能被100整除,例如4
2.年份能被400整除,例如400
ps:之前混淆,其实这两个条件并不冲突,这两个条件不是要求同时满足,是满足一个即是闰年。
cincout超时
cin和cout我都遇到了超时的情况…而且耽误了大量的时间,再也不想用了…
常见字符串处理
判断字符是否为数字或字母
常见的判断字符穿是否为数字或字母都是在if中进行复杂的书写,因为字母包括大小写,且是一段闭区间,可以使用一个函数来直接判断。
#include <cctype>
if(isalnum(s[i])){
/*code*/
}
大小写转换
一般遇到大小写转换要先判断,然后减去或加上ascii码表上的值,其实过程比较繁琐,可以简单使用tolower/toupper完成。此函数会自动识别是否为英文字符,若不是英文字符不做变换。
#include <cctype>
s[i] = tolower(s[i]); //转换成小写
s[i] = toupper(s[i]); //转换成大写
string中的.erase用法
1.括号内迭代器,删除单个元素。
str.erase(str.begin() + n);
2.括号内单个数字,删除该位置以后所有元素。
3.括号内两个数字,第一个数字仍然代表位置,第二个数字代表长度。
string中的.erase与.substr方法
之前大概都知道.erase是用来消除元素的,.substr是用来截取子串的,但是今天用的时候发现不太会用,特此注明一下,至于为什么把这两个函数写在一起,是因为他们的用法相似。函数都有两个参数要传。
分别是:position(pos), length(len)
表示:要处理的位置(从0开始),处理的长度
string str = "0123456";
string sub = str.substr(2,2);
// output:23
str.erase(3,1);
// output:012456
//总结也发现sub一般采用接收返回值的方法,erase通常不适用接受值直接对原字符串进行改变。
string中的.find方法详解
用来寻找一个字符串中是否含有子串或子字符,常使用如下:
//默认从左开始找
母串.find(子串或子字符)!=string::npos
//从右开始找
母串.rfind(字串或字符串)!=string::npos
其中 string::npos 表示没有找到。
数字字符(int)对字符(char)的相互转换
由于int+或-char类型可以直接转换为char类型,所以常借助ascii码表数字排位第一的’0’字符来转换:
//将1转换为'1'
char yi = 1+'0';
//将'1'转换为1
int yi = '1'-'0';
数字字符串(int)对字符串(string)的相互转换
#include<sstream>
//数字转换成字符串
void i2s(int x,string &str){
stringstream ss;
ss << x;
ss >> str;
}
//字符串转换成数字
void s2i(int &x,string str){
stringstream ss;
ss << str;
ss >> x;
}
接收不确定的输入长度回车截止
有时会输入不确定个数的数字,以空格隔开,以回车结束,由于c没有java那样直接对字符串分割的函数
#include<sstream>
const int Maxn = 10000;
int data[Maxn];
string s;
getline(cin,s); //先按行接收 若是之前有输入记得用 getchar()接收回车
istringstream iss(s);
string temp;
//getline 其实自带分割
//但是第一个参数需要使用istringstream
//第三个参数确定分割依据
//第二个参数确定存入哪里
while(getline(iss,temp,' ')){
//进行存储
s2i(tmp,data[index++]);
}
以上方法确实简单明了,但是我个人感觉不太好记忆,如果并不需要记录整行可以使用while检测回车字符输入,例如:
while(cin >> key){
char c = getchar();//接受回车和空格
v.push_back(key);
if (c == '\n')
{
break;
}
}
C语言中接受参数忽略及动态输出
int a;
char b[10];
scanf("%d %*s",&a,b); //a会被接收 b不会
printf("%*s",10,s); //输出字符串s,不足的地方用s补空格
stl模版中的set的一些坑
patA1076中,我需要一个来检测是否出现过的方法,这时候我想到了集合标准库,没想到中坑了,当数据量变大时出现了超时,原因在于我找寻一个元素是否在set中出现过使用的是如下方法:
if(s.find(x) == s.end())
//这样的方法固然可以判断,但是每次都需要遍历一遍集合元素,这就上升了logN的时间复杂度
//但其实完全可以用一个布尔类型的数组来确定
bool visit[Maxn] = {false};
//这样就将复杂度变为1
set的查找,与string找子串的string::npos不同,当find找不到会得到end的迭代器,所以当要在set中进行查找操作应该是:
for (auto it = v[x].begin();it != v[x].end(); it++) {
if (v[y].find(*it) == v[y].end()) {
//当找到.end表示未找到。
nt++;
}
else
nc++;
}
有关迭代器的使用
以map型迭代器为例:
for (map<string,int>::iterator it=m.begin();it!=m.end():it++ )
{
//迭代器的使用需要注意的点有三,首先是定义的时候要说明类型,和stl模版类型相同
//其次是从.begin()起步,!=.end()为结尾
//最后不要拼错...
}
在之后的学习中我发现map string,int ::iterator可以直接写成auto。
结构体的多字段、多记录排序
结构体的多字段、多记录排序时,需要为sort函数重新写一个比较函数cmp;
cmp的书写遵循几点规律:
1.bool类型的返回值,且通常采用如下简写:
bool cmp(int &x,int &y){
return x>y;
//cmp函数的含义,如果返回值是 True,表示 要把 序列 (X,Y),X放Y前。
}
2.多字段排序采用if else结构:
bool cmp(node a,node b){
if(a.x != b.x) return a.x<b.x;
else if(a.y != a.y) return a.y<b.y;
else if(a.z != a.z) return a.z<b.z;
else return a.p < b.p;
}
string的贪心排序问题
今天做PAT的时候A1038这个题大意是想组成最短的号码,典型的贪心算法,我一开始完全是自己想每一位确定最小找,后来发现cmp函数太nb了,完全可以代替…二十行代码干出来30分的题:
bool cmp(string a,string b){
return a+b < b+a;
}
//直接排序完成杀死比赛...
数学知识点
找1~n素数
普通暴力求解
#include <cmath>
for(int i=2;i<=n;i++){
bool judge = true;
for(int j=2;j<=sqrt(i);j++){
if(i%j==0){
judge = false;
}
}
if(judge)
sushu[index++]=i;
}
有一点需要注意的是,0,1并不是素数,若是数据范围是自然数需要先对两个数进行排除。
素数筛法
思路:对于任意一个合数一定可以分解成多个素数的乘积。
做法:既然每个合数必然能分解成多个素数的乘积,那么在搜索到一个素数的时候我们就把它的倍数标记为合数。
for(int i=2;i<=n;i++){
if(p[i]==0){
sushu[index++]=i;
for(int j=2;j*i<=n;j++)
p[j*i]=1; //p中标记的都是合数 //动态规划
}
}
线性筛法
思路:在上一种筛法中6会被2,3晒掉两次,浪费了时间。
做法:将每个合数表示为一个素数乘以一个正整数的形式。
时间复杂度O(n)
for(int i=2;i<=n;i++){
if(p[i]==0)
sushu[index++]=i;
for(int j=1;j<=index && i*sushu[j]<=n;j++){
p[i*sushu[j]]=1;
//当遇到最小的质数是i的因数时,break
//因为他已经有最小素数组成,而我们每次都是从最小开始遍历,避免遗漏
if(i%sushu[j]==0) break;
}
}
二分法查找元素
二分法查找元素虽然早在去年就学过,但我一直不怎么常用,说是简单其实还是有一些要注意的点:
首先要明确二分查找是对严格递增的数组进行查找,也就是说要排序且去重。
其次要明确边界left、right的变换过程,是变换到mid的左一个或右一个,而不是和mid一个位置。
最后要明确出口条件那就是left始终在right左边,若不满足则退出while循环。
具体实现代码如下:
//二分查找
int ans = -1;
int left = 0;
int right = n-1;
int mid = (left+right)/2;
while(left <= right){
if(v[mid] == m) {
ans = mid;
break;
}
else if(v[mid] > m){
right = mid -1;
mid = (left+right)/2;
}
else if(v[mid] < m){
left = mid +1;
mid = (left+right)/2;
}
}
二分查找不仅是用在找当个数据上,涉及一段非严格单调的数列,我们可以采用累加形成严格递增的数列后,再使用二分查找,此时应该注意mid变动的条件并不是仅看mid的值了,是需要看mid值与左区间的关系。
快速排序
快排属于基础的不能再基础的排序算法之一,其一般复杂度是O(nlogn),在最坏情况时(数排列随机性低)也会是O(n^2)。快速排序算法分为两个部分:
1.结合two points思想,完成当前数组的划分,使得选定元素左边的数都比其小,选定元素右边的数都比其大,具体代码如下:
ps:要注意时从左边开始判断,并且在while循环内部也要判定left小于right
//二分查找
int Partition(int a[],int left,int right){
int temp = a[left];
//必需先从左开始看不能搞反
while(left<right){ //在while内部也要检测left<right
while(a[right]>temp && left<right){right--;}
a[left] = a[right];
while(a[left]<temp && left<right){left++;}
a[right] = a[left];
}
a[left] = temp;
return left;
}
2.当快速排序的left不小于right了,也即我排序的区间已经是1(left、right指着一个数)就停止排序了,具体代码如下:
ps:要注意的是排序子区间时已经不需要考虑划分好区间的这个主元了
void quickSort(int a[],int left,int right){
if(left<right){
int pos = Partition(a,left,right);
quickSort(a,left,pos-1); //不需要考虑主元pos
quickSort(a,pos+1,right);
}
}
快速幂用于求a^b%m
时间复杂度O(logb)
long long binaryPow(long long a,long long b,long long m){
if(b == 0) return 1;
if(b%2 == 1) return a*binaryPow(a,b-1,m)%m;
else{
long long ans = binaryPow(a,b/2,m);
return mul * mul % m;
}
}
其实就是二分的思想。
辗转相除法(欧几里德算法)求最大公约数(gcd)
求最大公约数的简洁代码如下,有了最大公约数也可以求最小公倍数。
//最大公约数
int gcd(int a,int b){
return a%b==0?b:gcd(b,a%b); //辗转相除法中没有除法,均做余运算
}
//最小公倍数
int x = a*b/gcd(a,b);
互质问题
两个数x,y如果互质,那么 x*y-x-y之后的数都是可以用x、y的整数倍拼出来的,互质的含义也就是用辗转相除法得到的最大公约数是1.
而多个数的互质可以两两来运算,先得到两个数的最大公约数,再用这个数和之后的数用辗转相除法,若最后结果是1,则表示多个数互质。
cmath库中的常用函数
cmath中有许多常用来数学计算的函数,这里做一个统一复习:
#include <cmath>
fabs(double x); //取double型绝对值。
floor(double x); //向下取整 floor(5.2) = 5 floor(-5.2) = -6
ceil(double x); //向上取整 ceil(5.2) = 6 ceil(-5.2) = -5
pow(double r, double p); //返回r的p次方,不过现在我一般用快速幂求解了
sqrt(double x); //返回x的算术平方根
log(double x); //返回x以e为底的对数
//若想变换成自己想要的底则需要用到换底公式 : logab = logeb/logea
round(double x); //对x四舍五入取整
//圆周率的精确表示 pai = arccos(-1)
double pi = acos(-1.0)
数列知识
//等差数列:
an = a1 + (n-1)d;
Sn = n*(a1-an)/2
//等比数列:
an = a1q^(n-1);
Sn = a1(1-q^n)/(1-q);
10进制转换为c进制的问题
之前我都是采用递归调用,那种方法在遇到“大数”就不行了,这里的大数不是说这个数字本身有多大,而是进制转换后数字所占位数太多,最后溢出。
比如一个正常大小的int位数字 9876543 ,如果转换为 2 进制,longlong也装不下,还是老老实实的用数组来求最后反序输出模拟手算比较靠谱。
ps:这里之所以不用string类字符串是因为涉及余、除运算,字符串换来换去的真的很不方便,还不如直接用int型数组。
do{
ans[num++] = y % c;
y = y/c;
}while(y != 0);
for(int i=num-1;i>=0;i--)
cout<<ans[i];
找质因数
struct factor{
int x,cnt;
}fac[10];
考虑到前10个质数的乘积已经大于int的范围了(2~39),我们取10个就够了。
有一个很强的定理:对于一个整数n来说,如果它存在[2,n]范围内的质因子,要么这些质因子全部小于等于sqrt(n),要么只有一个质因子大于sqrt(n),其余均小于等于sqrt(n)。
ps:一般找质因数的题要对1做单独考虑;
质因数总结:
1.打1-sqrt(n)内的素数表。
2.对于n,使用每一个素数表中的元素去试能否被整出,如果能被整除就初始化,并把x放入fac数组中,cnt先初始化为0。
3.与2在一个for循环中,使用一个while循环找出n到底能被选定素数整除多少次,对cnt++,同时n/=p[i],在for循环最后fNum++。
4.因为有可能存在有一个质因数大于sqrt(n),所以要检查一下n是否等于1了,如果n的质因数全部被找出来了n应该是为1,因为每次都除,所以不为1时可以肯定是有一个大于sqrt的数,此时只需要将这个n直接记录为一个f中的x,再将这个f的cnt=1,同时要记得fNum++,方便之后遍历。
源码如下:
//
// main.cpp
// PAT_A1059
//
// Created by VachelChen on 2020/3/7.
// Copyright © 2020 VachelChen. All rights reserved.
//
#include <iostream>
#include <cmath>
using namespace std;
struct factor{
int x,cnt;
}f[10];
const int MAXN = 10000000;
int p[MAXN];
int pNum = 0;
int fNum = 0;
bool judgePrime(int x){
for(int i=2;i<=sqrt(x);i++){
if(x%i == 0)
return false;
}
return true;
}
int main(int argc, const char * argv[]) {
int n,m;
cin >> n;
if(n == 1){
cout<<"1=1"<<endl;
return 0;
}
m = n;
for(int i=2;i<=sqrt(n);i++){
if(judgePrime(i)){
p[pNum++] = i;
}
}
for(int i=0;i<pNum;i++){
if(n % p[i] == 0){
f[fNum].x = p[i];
f[fNum].cnt = 0;
while (n % p[i] == 0) {
f[fNum].cnt++;
n = n / p[i];
}
fNum++;
}
}
if(n!=1){
f[fNum].x = n;
f[fNum].cnt = 1;
fNum++;
}
cout<<m<<"=";
if(f[0].cnt != 1) cout<<f[0].x<<"^"<<f[0].cnt;
else cout<<f[0].x;
for (int i=1; i<fNum; i++) {
if(f[i].cnt != 1) cout<<"*"<<f[i].x<<"^"<<f[i].cnt;
else cout<<"*"<<f[i].x;
}
cout<<endl;
return 0;
}
快速求n!中的质因数p的个数
这个问题我还没遇到过,具体遇到这样的题应该也不会对时间有要求吧…?
这个诀窍在于不要一个个的加答案,n!的质因数p的个数是 (n/p + n/p^2 + n/p^3 …),详细代码如下:
int workOut(int n,int p){
int ans = 0;
int op = p;
while( n/p>=1 ){
ans += n/p;
p = p * op;
}
return ans;
}
利用这个方法还可以很快算出: n!的末尾有多少个0
由于问题等价为 n!有多少个10作为因子,而又等于质因子中5的个数,所以直接 workOut(n,5) 即可。
计算Cmn(从m个中取n个的排列组合算法)
一直以来排列组合问题都因为他数学形式的特殊性不好表示从而不好被程序求解,而且通过粗略计算可以发现,如果使用公式法那么在m=20之后的数字会超过long long,这里给出递推的方法:
从m个中取n个 = 从m-1个中取n个+从m-1个中取n-1个
而 Cn0 = Cnn = 1
对时间要求不严的写法:
long long C(long long n,long long m){
if(m == 0||m == n) return 1;
return C(n,m-1)+C(n-1,m-1);
}
有没有一种类似斐波那契的感觉?
所以还有一种动态规划牺牲空间挽救时间的对时间要求严格的写法:
long long res[67][67]={0};
long long C(long long n,long long m){
for(int i=0;i<m;i++){
for(int j=0;j<=i;j++){
if(j == 0 || i == j)
res[i][j] = 1;
else
res[i][j] = res[i-1][j]+res[i-1][j-1];
}
}
}
1~n中出现1的个数
可以想见,若不考虑时间复杂度是一个非常简单题。如何简化时间呢,一开始我种想从前面的结果中找规律但无果。才考了柳神代码发现了有一种比较巧妙的做法。
从第一位到最高位的情况累加。
1.当前位要是为0那该位置在过程中出现1的情况就只有left乘以a数的情况。
2.当前位要是为1那该位置在过程中出现1的情况是left乘以a+右边从0~right。
3.其他情况就是左边从0~left此,但是还需乘以a。
具体代码:
#include <iostream>
using namespace std;
int main() {
int n, left = 0, right = 0, a = 1, now = 1, ans = 0;
scanf("%d", &n);
while(n / a) {
left = n / (a * 10), now = n / a % 10, right = n % a;
if(now == 0) ans += left * a;
else if(now == 1) ans += left * a + right + 1;
else ans += (left + 1) * a;
a = a * 10;
}
printf("%d", ans);
return 0;
}
0到n-1的排列顺序
交换排序swap。
首先假设任意两个数可以交换,需要交换的次数其实就是(圈长-1)的总和。
圈的概念是指:例如a在b的位置,b在c的位置,c在a的位置这样就构成一个圈,这个圈包含m个元素就需要交换m-1次,每次都可以把一个元素放在正确的位置上。题目含义等价于找圈。
但是由于题目的意思是只能用0来交换,就有两种情况:
1.若果我们找到了一个包含0的圈,需要m-1次。
2.若果0不在圈中,我们就需要把0换进来,最后再换出去,这样就比上一种情况多2次,所以需要m+1次。
核心代码:
int give(int x){
int r = 0;
bool c = false;
for (; !mark[x]; r++)
{
if (x == 0)
{
have = true;
}
mark[x] = true;
x = a[x];
}
return have?(r-1):((r<=1)?0:(r+1));
}
这个题与跳蚱蜢相比之所以不用BFS是因为跳蚱蜢的移动距离是有限的,而此题的交换是没有记录限制的交换,所以若用BFS那所造成的可能将极多。
模拟类型
一般模拟的题型都是水题,但是今天遇到了一个之前在比赛中遇到的模拟问题,写了好长时间,所以在此记录一下。
大致题意是有n个窗口,每个窗口前面能拍m人的队,每个新来的人都选择最短的队排,问每个人的结束时间。
这类问题我的做法是,首先人要是一个结构体,包含id和耗时,之前尝试直接用数组但是发现之后还是需要调用其id,所以还是结构体方便一些,然后就是queue[]队列数组,队列数组在每个窗口前,队列是person属性(队列中的每个元素都是一个人),一切准备就绪后就使用for循环进行模拟实践的操作,其实这个方法我的灵感是来自蓝桥杯里的高斯日记,关于时间流逝的题目其实使用一个基础单位来循环是一个不错的选择。
关于这类排队的问题有一坑就是最后一个人只要在服务时间内开始了服务就一定要服务完,这也符合逻辑。
参考代码如下:
//
// main.cpp
// PAT_A1014
//
// Created by VachelChen on 2020/5/19.
// Copyright © 2020 VachelChen. All rights reserved.
//
#include <iostream>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1024;
int n,m,k,q;
int firstWindows[21];
struct downTime{
int h;
int m;
};
struct person{
int id;
int process;
downTime dt;
person(){
dt.h = -1;
}
}p[maxn];
queue<person> windows[21];
void coming(int init){
int x=1;
int queueNumber = 1;
int outLine = 0;
while (x<=init && x!= k+1) {
windows[queueNumber].push(p[x]);
queueNumber = (queueNumber+1) % (n+1);
if(queueNumber == 0) queueNumber++;
x++;
}
for (int i=1; i<=540; i++) {
for (int j=1; j<=n; j++) {
if (!windows[j].empty()) {
if (firstWindows[j]>0) {
firstWindows[j] --;
}
else{
firstWindows[j] = windows[j].front().process;
firstWindows[j] --;
}
}
}
for (int j=1; j<=n; j++) {
if (firstWindows[j] == 0) {
int number = windows[j].front().id;
p[number].dt.h = i / 60 + 8;
p[number].dt.m = i % 60;
windows[j].pop();
outLine++;
firstWindows[j] = -1;
}
}
while (x <= k && outLine>0) {
int minLine = m;
int minWindow = 0;
for (int j=1; j<=n; j++) {
if (windows[j].size() < minLine) {
minWindow = j;
minLine = (int)windows[j].size();
}
}
windows[minWindow].push(p[x]);
x++;
outLine--;
}
}
int maxtime = -1;
for (int i=1; i<=n; i++) {
if (firstWindows[i] > 0) {
maxtime = max(maxtime,firstWindows[i]);
}
}
for (int i=541; i<=maxtime+540; i++) {
for (int j=1; j<=n; j++) {
if (firstWindows[j]>0) {
firstWindows[j] --;
}
}
for (int j=1; j<=n; j++) {
if (firstWindows[j] == 0) {
int number = windows[j].front().id;
p[number].dt.h = i / 60 + 8;
p[number].dt.m = i % 60;
windows[j].pop();
firstWindows[j] = -1;
}
}
}
}
int main(int argc, const char * argv[]) {
memset(firstWindows, -1, sizeof(firstWindows));
scanf("%d %d %d %d",&n,&m,&k,&q);
for (int i=1; i<=k; i++) {
p[i].id = i;
scanf("%d",&p[i].process);
}
coming(n*m);
for (int i=1; i<=q; i++) {
int y;
scanf("%d",&y);
if(p[y].dt.h == -1){
cout<<"Sorry"<<endl;
}
else{
printf("%02d:%02d\n",p[y].dt.h,p[y].dt.m);
}
//cout<<"ok"<<endl;
}
return 0;
}
排队问题模拟
通常涉及时间流逝的题目常用以秒或天这样题目中的最小时间单位来模拟流逝,从而达到模拟流程的效果,今天遇到一些排队论问题,过程不需要模拟而是找相应的时间差,这也是一种新的解决思路。
//完成输入以及对时间的排序
//为每一个窗口置一个起始时间
for (int i=1; i<=k; i++) {
ttime[i] = starttime;
}
//遍历每一位顾客
for (int i=0; i<n; i++) {
//来的太晚了直接ban掉
if (person[i].arrive > endtime) break;
else{
//找到柜台处时间最小的一个柜台
int minserver = endtime;
int winnumber = 0;
for (int j=0; j<k; j++) {
if (window[j] < minserver) {
minserver = window[j];
winnumber = j;
}
}
//看一下这个顾客的状态是柜台等人还是人等柜台
int servertime = max(person[i].arrive,minserver);
//只有人等柜台才需要计算等待时间
total += (servertime - person[i].arrive);
//得到服务开始的时间后,柜台的时间变为服务开始时间+服务时间
window[winnumber] = servertime + person[i].p;
}
}
链表题型
今天在复习算法时在PAT题目中看到了基本一模一样的我在PAT考场遇到的链表算法题,当时真的是没认真对待,原来这个有着么深的套路,在这里记录做总结。
常见的是叫静态链表,固定模版如下:
第一步,定义静态链表结点属性:
const int maxn = 100010; //根据给定数据的位数来确定,大一位即可
struct node{
int address,key,next; //包含指针位置,指针值,指向地址
bool flag; //一般用来遍历一遍给的结点来确定哪些结点不在链表上
}n[maxn];
第二步,初始化flag:
for (int i = 0; i < maxn; ++i)
{
n[i].flag = false;
//之前多虑了,这里时间复杂度应该是1
}
第三步,根据首地址start来标注flag:
int cnt = 0; //记录链表上的节点个数
for(int i=start;i != -1;i = n[i].next){ //这就是静态链表采取hash的好处
n[i].flag = true;
cnt++;
}
第四步,排序结点,使链表上的结点向左并,没在链表上的结点在后面:
bool cmp(node a,node b){
if(a.flag == false || b.flag == false)
return a.flag > b.flag; //大于成立则交换
else
return a.key < b.key;
}
sort(n,n+maxn,cmp);
第五步,具体看题目要求:
接下来要具体看题目要求,值得注意的是考虑:
1.链表为空的情况。
2.使用“%05d”补充非 -1 的数字的0的情况。
一、枚举及全排列
数字位全排列
对一串指定长度为n的数字要对每一位做全排列的话,若直接使用n位最小数字到n位最大数字的一个for循环,在取出每一位上数字时会较为麻烦,这时候推荐采用n个for循环,在每一个循环中添加约束条件会比较清晰。
//取各位都不一样的六位数
//推荐做法:
for (int i = 1; i < 10; ++i) {
for (int j = 0; j < 10; ++j) {
if (j != i)
for (int k = 0; k < 10; ++k) {
if (k != i && k != j)
for (int l = 0; l < 10; ++l) {
if (l != i && l != j && l != k)
for (int m = 0; m < 10; ++m) {
if (m != i && m != j && m != k && m != l)
for (int n = 0; n < 10; ++n) {
if (n != i && n != j && n != k && n != l && n != m) {
long long x = i * 100000 + j * 10000 + k * 1000 + l * 100 + m * 10 + n;
if (check(x, x * x)) {
cout << x << " " << x * x << endl;
}
}
}
}
}
}
}
}
//我的做法
for(long long i=123456;i<=987654;i++)
{
liu = i%10;
wu = (i-liu)%100/10;
si = (i-wu*10-liu)%1000/100;
san = (i-si*100-wu*10-liu)%10000/1000;
er = (i-san*1000-si*100-wu*10-liu)%100000/10000;
yi = (i-er*10000-san*1000-si*100-wu*10-liu)/100000;
if(liu==wu || liu==si || liu==san || liu==er || liu==yi || wu==si || wu==san || wu==er || wu==yi || si==san || si==er || si==yi || san==er || san==yi || er==yi)
continue;
//····
}
全排列
全排列是一个常见操作,其实一个函数就可以解决:
#include<string>
int main(int argc, char const *argv[])
{
string s="223344AA" //首先给出一个字符串
do{
if(check(s)){ //在check函数中对字符串进行检查
cout<<s<<endl;
}while(next_permutation(s.begin()s.end())); //模版
}
return 0;
}
特殊去重
手环排列问题,要把s+s以及s+s的反向加入vecter。
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector <string> v;
int main(int argc, const char * argv[]) {
string s = "rrrwwwwyyyyy";
int ans=0;
do{
int i;
for(i=0;i<v.size();i++){
if(v[i].find(s)!=string::npos) break;
}
if(i!=v.size()) continue;
ans++;
string s2=s+s;
v.push_back(s2);
//翻转函数的用法
reverse(s2.begin(), s2.end());
v.push_back(s2);
}while(next_permutation(s.begin(),s.end()));
cout<<ans<<endl;
return 0;
}
二、大数运算
避免大数运算
若是只涉及两个long long型数据相加比较大小的问题,不需使用大数运算,因为相加可能会导致益出,但是程序是可以顺利运行而不会报错的,这里需要掌握的是两个正数相加若益出是变成负数,两个负数相加益出是0或正数,由此作为特殊情况方可简单进行判断。
填空题大数运算技巧
蓝桥中有填空题,不像ACM时全部要求提交源程序,这就可以利用其他语言来取个巧,比如 Python 是支持大数运算的:
Python 不一定在考试机上有,但我个人认为 Python 是最方便的,只需要最简单的idle即可完成运算:
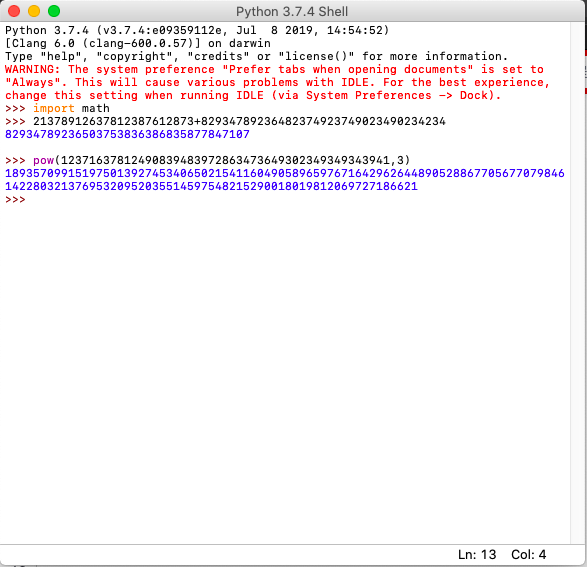
接下来介绍使用c/c++的处理方法:
其原理就是使用数组来代替存储,使用string的话计算减法借位时会比较不方便。
常用数据结构:
struct bign{
int d[1000];
int len;
//因为结构体中有数组,定义的时候需要初始化一下。
bign(){
memset(d,0,sizeof(d));
len = 0;
}
};
输入处理:
以字符串记录,记录成bign形式,同时会导致整数的高位会变成低位,可以做一下处理。
bign change(string str){
bign a;
a.len = str.size();
for(int i=0;i<a.len-1;i++)
a.d[i] = str[a.len-i-1] - '0';
return a;
}
高精度加法:
bign add(bign a,bign b){
bign c;
int carry = 0;
for(int i=0;i<max(a.len,b.len);i++){
int temp = a.d[i] + b.d[i] + carry;
c.d[c.len++] = temp%10;
carry = temp/10;
}
if(carry!=0){
c.d[c.len++] = carry;
}
return c;
}
高精度减法:
bign sub(bign a,bign b){
bign c;
int carry = 0;
for(int i=0;i<max(a.len,b.len);i++){
if(a.d[i]<b.d[i]){
a.d[i+1]--;
a.d[i] += 10;
}
c.d[c.len++] = a.d[i] - b.d[i];
}
while(c.len >=2 && c.d[c.len-1] == 0)
c.len--;
return c;
}
long long的所能容纳的长度
一般大数运算在加减之间比较多,设计乘除难度比较大,所以一定要很好的区分大数,我理解大数是用long long都不够装的数字:
// long long 占8字节
// 8字节=64位 其中第一位勇于存放符号
-2^63~2^63
2^63 = 922 337 203 685 477 5807 (上限大约是20位十进制数)
简单记为:int 10位 long long 20位
三、排序
既然都是练习了也别老想着用sort排序了,复习一下基础。
冒泡排序
#include <iostream>
using namespace std;
int main(int argc, const char * argv[]) {
int a[10] = {3,65,13,67,96,24,22,74,34,25};
for(int i=0;i<10-1;i++){
for(int j=0;j<10-i-1;j++){
if(a[j]>a[j+1]){
int temp;
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
for(int i=0;i<10;i++)
cout<<a[i]<<"\t";
return 0;
}
四、图论
基础图论
图的存储
1.邻接矩阵
用二维数组来存储,虽然比较简单但一般是长宽需小于1000,避免越界。
2.邻接表
用链表实现与该点有链接的点。一般使用vector工具实现邻接表。
开一个变长数组vector[N]:
std::vector<int> v;
//不考虑权值
//考虑权
struct node
{
int node;
int weight;
};
std::vector<node> v;
DFS
完成重复子问题的优化
1.记忆型递归
这个位置+状态是已经遇到过的,进行存储,避免走重复的路。
//设置缓存
#include<cstring>
long long cache[xMax][yMax];//也可以根据位置+状态调整为多维;
//得用返回值的形式
long long dfs(int x,int y){
//查缓存
if(cache[x][y] != -1) return cache[x][y];
//为了给cache存当前节点到目标的有效值,需要在每次迭代中归零ans
long long ans = 0;
//dfs过程.....
//写缓存
cache[x][y] = ans;
}
int main(int argc, char const *argv[])
{
memset(cache,-1,sizeof(cache));
dfs(x,y);
return 0;
}
dfs解决类bfs问题
在刷蓝桥的题目的时候,已经不止一次遇到一种特殊的dfs统计,类似于:
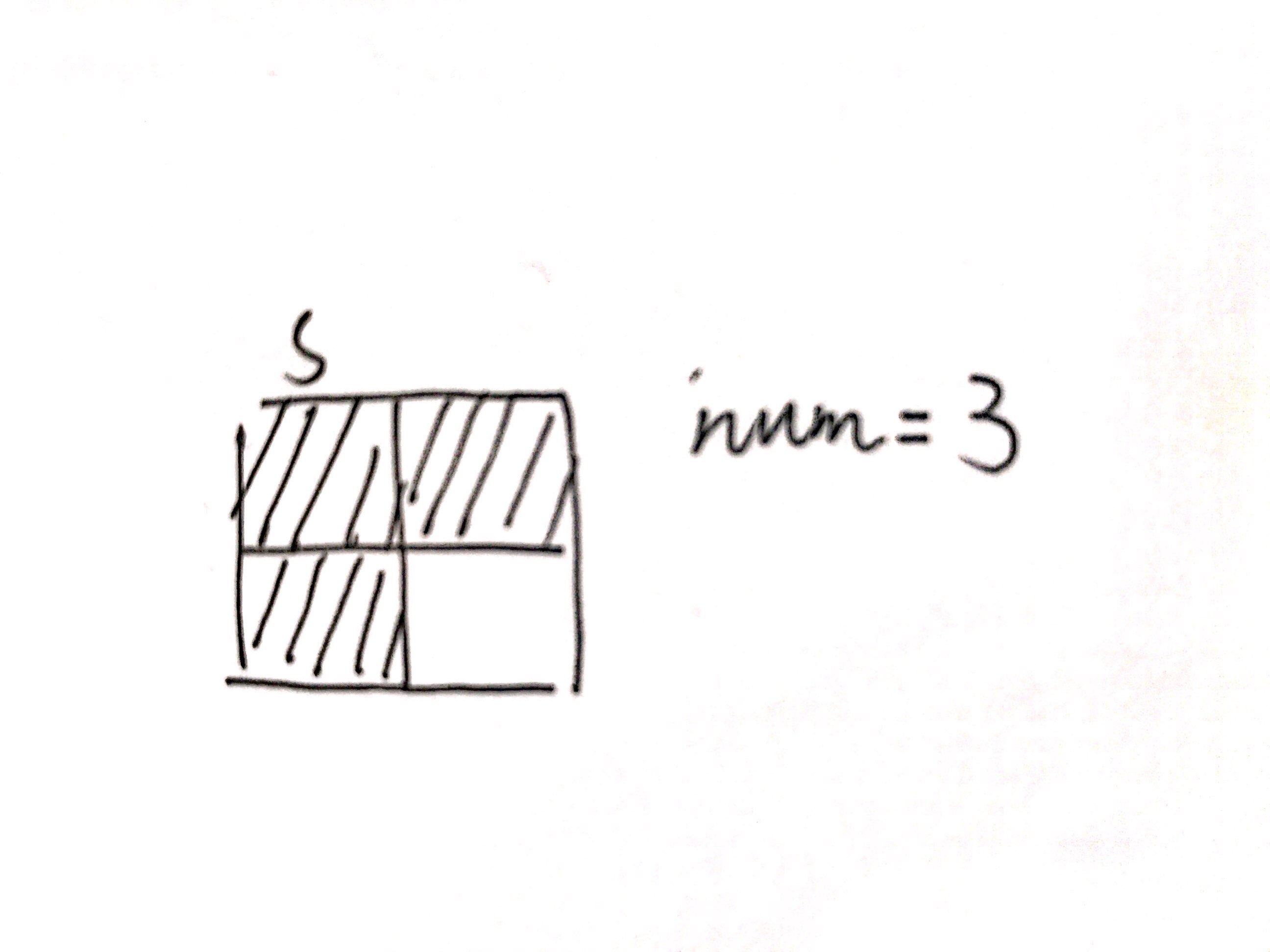
若从左上角是起点,则永远无法用dfs遍历出这种形状的结果,这时有人会说为什么不使用bfs,bfs虽然能得到这种结果,但又只能得到这种结果,本身还不具有计数功能,就是十分蛋疼。
面对这种情况,我在网上看到了一篇还不错的帖子,其方法是:全排列+dfs。
大致思路是:
我先把所有的cell在数组中用0,1标出来,其中1代表选中的cell,再使用next_permutation来全排列,对每一种排序结果检测其连通性,检测方法就是选中一个cell,按照1的地图来走,若能累计加和为5,则说明可以连通,这种方法还不用去重,可谓美哉。
粘贴一个解决2016_剪格子的代码:
如【图1.jpg】, 有12张连在一起的12生肖的邮票。 现在你要从中剪下5张来,要求必须是连着的。 (仅仅连接一个角不算相连) 比如,【图2.jpg】,【图3.jpg】中,粉红色所示部分就是合格的剪取。
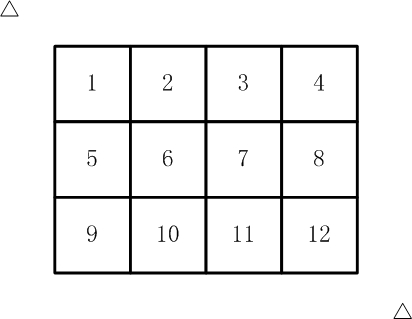
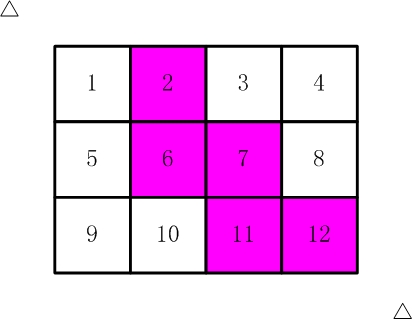
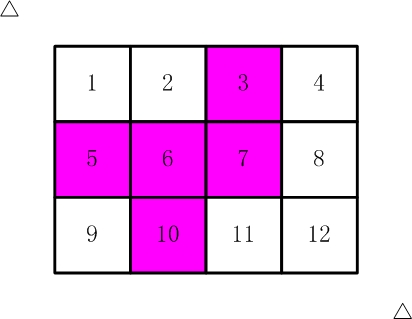
#include <iostream>
#include <cstring>
#include <algorithm>
#include <sstream>
#include <vector>
using namespace std;
int a[3][4];
int visit[3][4];
int num;
bool flag;
vector<string> v;
string i2s(int x){
stringstream ss;
string s;
ss << x;
ss >> s;
return s;
}
void dfs(int x,int y){
visit[x][y] = 1;
num++;
if(num == 5){
flag = true;
return ;
}
if(x<2 && !visit[x+1][y] && a[x+1][y]) dfs(x+1, y);
if(x>0 && !visit[x-1][y] && a[x-1][y]) dfs(x-1, y);
if(y<3 && !visit[x][y+1] && a[x][y+1]) dfs(x, y+1);
if(y>0 && !visit[x][y-1] && a[x][y-1]) dfs(x, y-1);
}
int main(int argc, const char * argv[]) {
int value[12]={0,0,0,0,0,0,0,1,1,1,1,1};
int ans=0;
do{
int n=0;
memset(visit, 0, sizeof(visit));
for(int x=0;x<3;x++){
for(int y=0;y<4;y++){
a[x][y] = value[n++];
}
}
bool doubleJump = false;
for(int x=0;x<3;x++){
for(int y=0;y<4;y++){
if(a[x][y] == 1){
flag = false;
num = 0;
dfs(x,y);
doubleJump = true;
break;
}
}
if(doubleJump) break;
}
if(flag){
ans++;
}
}while(next_permutation(value,value+12));
cout<<ans<<endl;
return 0;
}
//答案116
//之前单用dfs做出来次啊25,bfs做到一半发现不对...
当然了,只有数目较小的时候才可以用全排列,比如2017_方格分割用全排列(36取18)在有限的时间根本算不出来….而是要使用下面这张减法
dfs解决类bfs问题的变形
由于17年这个题目的特殊要求,要求剪出两边的形状一样,我们考虑从中心开始的边的dfs。
//
// main.cpp
// 2017_方格分割
//
// Created by VachelChen on 2020/2/26.
// Copyright © 2020 VachelChen. All rights reserved.
//
#include <iostream>
#include <cstring>
using namespace std;
int visit[7][7];
int ans = 0;
void dfs(int x,int y){
if(visit[x][y]) return;
if(x == 0 || x == 6 || y == 0 || y == 6){
ans++;
return;
}
visit[x][y] = 1; //最后一个点一般不用标记,也就是说在满足情况的下方,不然无法标记回来...
visit[6-x][6-y] = 1;
dfs(x+1, y);
dfs(x,y+1);
dfs(x-1,y);
dfs(x,y-1);
visit[x][y] = 0;
visit[6-x][6-y] = 0;
}
int main(int argc, const char * argv[]) {
memset(visit,0,sizeof(visit));
dfs(3, 3);
cout<<ans/4<<endl;
return 0;
}
非直观图的DFS问题
今天做PAT_A1043,涉及多个非直观图的找最大权问题,做个记录:
1.对于一个值是否已经被存入map的检测可以使用:
if(!m[string]){
;
}
2.由于是非直观图,邻接矩阵仅表示两点是否相邻,因此DFS需要借助循环来实现。
void DFS(int x,...){
visit[x] = 1;
...;
for(int i = 0;i < N;i++){
if(g[x][i]>0){
g[x][i] = g[i][x] = 0; //避免堆成矩阵造成死循环。
if(visit[i] == false)
DFS(i,...);
}
}
}
图去掉一点后的连通性考虑
一开始还以为是并查集的问题,后来发现并查集对于father选择的随机性导致并不能很好的找到剩下的点。
参考代码后才发现是dfs问题:
首先需要明确的是,要将n个连通区域连接最少需要n-1条线。
其次由于可能存在并不是连通图的问题,dfs的过程是需要对所有未访问点遍历的,在这些点中以起点开始启动dfs,只要连通就遍历到最终节点为止。
这里遇到一个特别坑的问题,也解开了我一个很久的疑惑,网上有许多优秀代码都是使用了using namespace std;的,但是实际使用cin输入的却很少,在PAT_A1013中我遇到了超时情况,这时候我寻求大佬解答发现:
这里一定要用scanf输入而不是用cin输入。对于大量输入的操作,cin因为有同步机制所以会超时。
所以以后若是超时了可以先考虑一下换成scanf…或者是对于非string类数据直接scanf输入吧。
BFS
stl中queue常用函数
想要用好bfs,用stl模版库中的现成队列再方便不过,这里总结一下队列中的函数:
#include <queue>
queue <datatype> q;
q.empty(); //判断队列是否为空
q.size(); //访问队列q的元素个数
q.push(a); //讲一个元素a放入队列
q.front(); //返回队列的第一个元素
q.pop(); //移除队列的第一个元素
找迷宫出口、包括找最短迷宫出口这都是使用BFS来干的事
(说实话只在课本上学过,一直没遇到过BFS实战的题目,没想到第一次见就是在赛场上,真是教训)
BFS大致框架如下:
学习数据结构时都知道BFS和队列有关,DFS和栈有关,想着自己在使用DFS时基本根本没有使用到 stcak结构,后知后觉才反应过来自己用的递归不就是栈吗?而BFS在实战时似乎就必须要使用队列,一般不会选自己去创建队列,stl模版库它不香吗?
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn=100;
bool vst[maxn][maxn]; // 访问标记
//虽然在我使用dfs的时候不喜欢用方向向量,但发现还是使用方向向量比较简洁
int dir[4][2]={0,1,0,-1,1,0,-1,0}; // 方向向量
// 在走迷宫一类问题中,放入队列的就是位置信息
struct State // BFS 队列中的状态数据结构
{
int x,y; // 坐标位置
int Step_Counter; // 搜索步数统计器
};
State a[maxn];
bool CheckState(State s) // 约束条件检验
{
if(!vst[s.x][s.y] && ...) // 满足条件
return 1;
else // 约束条件冲突
return 0;
}
void bfs(State st)
{
queue <State> q; // BFS 队列,设置为结构体类型,可以在结构体中设置一下构造函数来赋值比较方便。
State now,next; // 定义2 个状态,当前和下一个
st.Step_Counter=0; // 计数器清零
q.push(st); // 入队
vst[st.x][st.y]=1; // 访问标记
//采用while来完成对地图的遍历
while(!q.empty())
{
now=q.front(); // 取队首元素进行扩展
if(now==G) // 出现目标态,此时为Step_Counter 的最小值,可以退出即可
{
...... // 做相关处理
return;
}
for(int i=0;i<4;i++)
{
next.x=now.x+dir[i][0]; // 按照规则生成下一个状态
next.y=now.y+dir[i][1];
next.Step_Counter=now.Step_Counter+1; // 计数器加1
if(CheckState(next)) // 如果状态满足约束条件则入队
{
q.push(next);
vst[next.x][next.y]=1; //访问标记
}
}
q.pop(); // 队首元素出队
}
return;
}
int main()
{
......
return 0;
}
模拟走迷宫
主干仍然是BFS框架,为了方便记录一般再使用一张地图(已经是第三次使用地图,第一次地图用来记录地形,第二次用来记录访问情况),而此时这里的地图用来记录:当到这个点时,是怎么从上一个点过来的
而一般对于填空题来说,答案是唯一的,当有多条路径可以选择时一般题目会强调按字典序排,对于BFS第一轮找到的一定是最短路径这不用多说,但是如何保证是最短的呢?一开始我还对这个问题有所纠结,后来仔细一想发现只要我调整BFS在四个方向的遍历顺序满足字典顺序,就可以达到目标效果。
附上2019_迷宫:
//下图给出了一个迷宫的平面图,其中标记为1 的为障碍,标记为0 的为可
//以通行的地方。
//010000
//000100
//001001
//110000
//迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这
//个它的上、下、左、右四个方向之一。
//对于上面的迷宫,从入口开始,可以按DRRURRDDDR 的顺序通过迷宫,
//一共10 步。其中D、U、L、R 分别表示向下、向上、向左、向右走。
//对于下面这个更复杂的迷宫(30 行50 列),请找出一种通过迷宫的方式,
//其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
//请注意在字典序中D<L<R<U。(如果你把以下文字复制到文本文件中,请务
//必检查复制的内容是否与文档中的一致。在试题目录下有一个文件maze.txt,
//内容与下面的文本相同)
//(每行50个数字,格式不对的话需要自己去调整)
/*
01010
00001
01111
01000
*/
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
#include <string>
using namespace std;
char a[31][51];
int visit[31][51]={0};
char where[31][51];
int n,m;
struct state{
int x,y;
state(int _x,int _y){
x=_x;
y=_y;
}
};
void bfs(){
queue<state> q;
q.push(state(0,0));
visit[0][0]=1;
where[0][0]='S';
while(!q.empty()){
state temp = q.front();
q.pop();
if(temp.x == n-1 && temp.y == m-1) break;
if(temp.x < n-1 && !visit[temp.x+1][temp.y] && a[temp.x+1][temp.y] != '1' ) {
visit[temp.x+1][temp.y]=1;
q.push(state(temp.x+1,temp.y));
where[temp.x+1][temp.y]='D';
}
if(temp.y > 0 && visit[temp.x][temp.y-1]!=1 && a[temp.x][temp.y-1]!='1') {
visit[temp.x][temp.y-1]=1;
q.push(state(temp.x,temp.y-1));
where[temp.x][temp.y-1]='L';
}
if(temp.y < m-1 && visit[temp.x][temp.y+1]!=1 && a[temp.x][temp.y+1]!= '1') {
visit[temp.x][temp.y+1]=1;
q.push(state(temp.x,temp.y+1));
where[temp.x][temp.y+1]='R';
}
if(temp.x > 0 && visit[temp.x-1][temp.y]!=1 && a[temp.x-1][temp.y]!='1') {
visit[temp.x-1][temp.y]=1;
q.push(state(temp.x-1,temp.y));
where[temp.x-1][temp.y]='U';
}
}
}
int main(int argc, const char * argv[]) {
// insert code here...
cin>>n; cin>>m;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++){
cin>>a[i][j];
}
bfs();
char ans[1000];
int ansindex=0;
int x=n-1,y=m-1;
while(where[x][y]!='S'){
ans[ansindex++]=where[x][y];
if(where[x][y] == 'D')
x=x-1;
else if(where[x][y] == 'U')
x=x+1;
else if(where[x][y] == 'R')
y=y-1;
else if(where[x][y] == 'L')
y=y+1;
}
for(int i=ansindex-1;i>=0;i--)
cout<<ans[i];
cout<<endl;
return 0;
}
状态演变问中间步骤
17年的跳蚱蜢我看着很懵,我一开始还想着要用dp来做,但是后来发现这个过程极其不规律,找不到递推方程,没想到又是一种bfs的题型。
经过某一种状态的演变,到达一个目标状态,问中间经历多少步,一般都是bfs。
说实话早应该想到的,这个和迷宫有一个类似点:都是求最少步数,但这个貌似脱离了图论我就没往那方面想,还是要学会抽象问题。
Dijkstra算法
经典的最短路算法,首先先归纳一下大概的书写过程:
涉及数据结构:
int n,G[maxv][maxv];
//n 表示图中node个数
//G 表示领阶矩阵
int d[maxv];
//d 表示从一个起始点开始到d[i]的最短路径
bool vis[maxv];
//表示这个点已经访问过
第一步,初始化,常用数组初始化方法:
//对于要初始化为0、-1的数组,可以使用memset来处理:
memset(a,0,sizeof(a));
memset(g,0,sizeof(g));
//对于其他值的初始化
fill(a,a+n;INF);
fill(G[0],G[0]+n*n;INF);
操作中主要对d[]数组进行初始化操作:
//初始化d均为最大距离
fill(d,d+N,INF);
//起点到自己距离是0
d[s] = 0;
第二步,过程梳理:
首先构想伪代码。
第一层要循环n次,因为每一个点都需要找到一个最短路径d[j],一切都是在该循环中处理;
第二层循环中要对现在的每个点都进行遍历,要找到现在d[j]最小的一个点,找最短路我必须保证之前的已经是最小的了再往后找;
与第二层并列的还有一层循环,当我找到了最小的d[j]对应的点后,我还需要对所有点进行一次遍历,这时候我是为了找到在图中与之前到的点连通,并且没有被访问过,并且之前找到的点与这条路求和的值小于现在的这个目标点,此时我就对这个点的d进行更新。
完整邻接矩阵代码:
int n,G[maxv][maxv];
int d[maxv];
bool vis[maxv] = {false};
void Dijkstra(int s){
fill(d,d+maxv,INF); //fill函数将整个d数组赋为INF
d[s] = 0;
for(int i=0;i<n;i++){
int u = -1,MIN = INF;
for(int j = 0; j < n; j++){
if(!vis[j] && d[j] < MIN){
u = j;
MIN = d[j];
}
}
if(u == -1) return; //不联通
vis[u] = true;
for(int v=0; v<n; v++){
if(!vis[v] && G[u][v]!=INF && d[u]+G[u][v]<d[v]){
//三个条件缺一不可,通常可以再起一个if写第三个条件用于Dij+dfs的情况
d[v] = d[u] + G[u][v];
}
}
}
}
若Dijkstra算法中要考虑最短路如何实现而不是最短路长度的问题,需要创建一个辅助数组pre[],用来存放每个节点的直接前驱,最后再用while逆向遍历,插入栈中,最后s.top()输出栈内元素。
Dijkstra与DFS的应用+
两者的应用主要体现在一个回溯上。因为Dijkstra只负责找到最短路径的值,其实并未说明路径来源,所以当要进行回溯操作时需要DFS的应用。在Dijkstra找最短路时起时也需要对原算法有一点小变形,如果说算法分为遍历+更新两部分的话,更新部分是需要重写的:
#include<vector>
vector<int> pre[maxn];
for (int v=0; v<n; v++)
{
if(!vis[v] && G[u][v]!=INF){
if (d[v] > d[u]+G[u][v] )
{
d[v] = d[u]+G[u][v];
pre[v].clear(); //通过设置一个前驱动态数组来找到路径
pre[v].push_back(u);
}
else if(d[v] == d[u]+road[u][v]){
pre[v].push_back(u);
}
}
}
此时每一个pre里面都是对应点的路径,但是应该是反着的。
在使用DFS搜索时,是从当前的这个最短路径的节点往回走找到根节点。
#include<vector>
vector<int> path,temppath;
//设定路径和暂时路径
void dfs(int x){ //当前节点
temppath.push_back(x);
if (x == 0)
{
//找到根节点后要进行的操作
temppath.pop(x); //吐出首节点
return ;
//这里要及时return 不然后面的for循环也会执行
}
for (int i = 0; i <= n; ++i)
{
for (int i=0; i<pre[x].size(); i++) {
dfs(pre[x][i]);
}
}
temppath.pop();
}
Floyd算法
Floyd算法用于求任意两点之间的最短路径长度,Dijkstra用于求起始点到剩下所有点的最短路径长度,时间复杂度为On3,基本上都是使用邻接矩阵实现。
算法思想:
构造便利所有点的三层循环,分辨得到i,j,k,k也就是所谓的中介点,若ik与jk连通,并且ik+jk的距离小于ij的距离时,ij距离定义为ik+ij。
代码实现:
for(int k=0;k<n;k++){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(dis[i][k]+dis[k][j]<dis[i][j] &&
dis[i][k] != INF &&
dis[k][j] != INF){
dis[i][j] = dis[i][k] + dis[k][j];
}
}
}
}
注意事项:必须将中间节点k放在最外层。
最小生成树算法
图类问题大概有两种,一种是最短路径问题,可以考虑使用Dijkstra与算法解决。第二种就是最小生成树的问题,一般采用prim和kruskal算法。
prim是针对点生成最小生成树,kruskal是针对边生成最小生成树。
prim
中心思想:每次从点中选取一个与集合S距离最小的变加入最小生成树。过程类似Dijkstra算法。区别在于:d[]含义不同,在prim中表示点到以访问集合S的距离,所以最后选择时不用考虑+的情况,直接用Guj与dj做比较。
kruskal
中心思想:每次选择图中最小的边,如果边两端的顶点在不同的连通块中,就把这条边加入最小生成树中。
对于如何判断两个端点处于不同的连通块,采用并查集的方法。
int father[N]; //并查集数组
int findFather(int x){//返回父亲值
while(x!=father[x]){
x = father[x]; //获得自己的父亲节点
}
return x;
}
//定义边
struct edge
{
int u,v;
int cost;
}E[maxe];
//n个顶点,m条边
int kruskal(int n,int m){
int ans = 0,Num_edge = 0;
for (int i = 1; i <= n; ++i) //并查集初始化
{
father[i] = i;
}
sort(E,E+m,cmp);//从小到大排序边
for(int i = 0;i < m;i++){
int faU = findFather(E[i].u);
int faV = findFather(E[i].v);
if(faU != faV){
father[faU] = faV;
ans += E[i].cost;
Num_edge++;
if(Num_edge == n-1) break;
}
}
if(Num_edge != n-1) -1;//无法连通时返回-1
else return ans;
}
五、树
二叉树的设置如下:
struct node{
int key;
node* left;
node* right;
};
二叉树的一些常用性质
1.二叉树的第k层上最多有2^(k-1)个节点
2.深度为k的二叉树最多有2^k-1个节点
完全二叉树的一些常用性质
1.节点i的子节点为2i和2i+1
2.节点i的父节点为i/2
二叉树的遍历
1.二叉树的遍历常见的是先(pre)、中(in)、后(post)序遍历,这些都是数据结构学过的就不再赘述,这里要提到一下层序遍历(level):
//其思想是采用队列的形式:
#include<queue>
using namespace std;
queue<node*> q;
void levelOrder(node* root){
q.push(root);
while(!q.empty()){
node* temp = q.front();
if(temp->left != NULL)
levelOrder(temp->left);
if(temp->right != NULL)
levelOrder(temp->right);
q.pop();
}
}
二叉树的重建
我们可以由中序遍历,配合先/后/层遍历中的一种来得到二叉树。
以先序遍历和中序遍历为例:
int pre[maxn];
int in[maxn];
//preL 先序左位置,preR 先序右位置,inL 中序左位置,inR 中序右位置。
node* pre_In(int preL, int preR, int inL, int inR){
node* root = new node;
root->key = pre[preL];
int i;
for(i=0; i<preR; i++){
if(in[i] == pre[preL])
break;
}
int numLeft = i - preL;
root->left = pre_In(preL+1,numLeft,inL,i-1);
root->right = pre_In(numLeft+1,preR,i+1,inR);
}
静态树
除了对熟悉的二叉树考察,还会对普通的非二叉树考察,由于子结点个数不确定,如果均开最大空间容易炸,所以使用vector如下:
//当有key时:
struct node{
int key;
vector<int> child;
}n[maxn];
例题有PAT_A1053题,已完成上传git,这是第一次使用:
vector<vector<int> > ans;
//这样的动态二维数组结构,比较屌,但是有个地方需要注意,就是之后使用sort函数的时候,要考虑每种情况,包括可能为空??否则会报段错误:
bool cmp(vector<int> a, vector<int> b){
//要记得判断a,b有一方为空的情况,否则会出现段错误 //小朋友,我有很多问号???
if(a.empty() || b.empty()){
return a.empty();
}
int i = 0;
int j = 0;
while (i<a.size() && j<b.size() && a[i] == b[j]) {
i++;j++;
}
if(a[i]>b[j])
return true;
if(a[i] == b[j] && a.size()>b.size())
return true;
return false;
}
二叉查找树
定义:
1.要么二叉查找树是一颗空树。
2.要么比其小在左结点,比其大在右结点。
其删除问题还是比较值得思考的,首先明确,删除的一个结点的方法:
1.首先遍历二叉树找到该结点。
2.找到结点后选择一种情况:
a.不存在左子树/右子树,直接删除。
b.存在左子树,去找寻左子树的直接前驱,删除这个结点(递归删除)
c.存在右子树,去找寻右子树的直接后驱,删除这个结点(递归删除)
//找到直接前驱
node* findMax(node* root){
while(root != NULL){
root = root->right;
}
return root;
}
//找到直接后驱
node* findMin(node* root){
while(root != NULL){
root = root->left;
}
return root;
}
3.接下来递归删除前驱/后驱节点。
void deleteNode(node* & root,int x){
if(root == NULL) return ;
if(root->val == x){
if(root->left == NULL && root->right== NULL){
root = NULL;
}
else if(root->left){
node* pre = findMax(root->left);
root->val = pre->val;
deleteNode(root->left,pre->val); //在左子树中删除节点pre
}
else{
node* next = findMin(root->right);
root->val = next->val;
deleteNode(root->right,next->val); //在右子树中删除节点next
}
}
else if(root-val > x){
deleteNode(root->left, x);
}
else if(root-val < x){
deleteNode(root->right,x);
}
}
二叉查找树+完全树
例题:PAT1064
二叉查找树保证的是left小,root中,right大,这样的大小次序类似于中序遍历的次序,所以当有一个序列需要变成查找树时,可以先对序列进行排序,然后使用中序遍历的方法对树中的元素依次填充。
代码如下:
#include <iostream>
#include <vector>
using namespace std;
const int maxn = 1010;
int n;
int tree[maxn],v[maxn];
int y=0;
void createMidTree(int root){
if(root >= n) return;
//由于是完全数,根节点冲0开始,因此只取小于n的节点。
createMidTree(root*2+1);
tree[root] = v[y++];
createMidTree(root*2+2);
}
int main(int argc, const char * argv[]) {
scanf("%d",&n);
if (n == 0) {
return 0;
}
for (int i=0; i<n; i++) {
scanf("%d",&v[i]);
}
sort(v, v+n);
//新建树
createMidTree(0);
printf("%d",tree[0]);
for (int i=1; i<n; i++) {
printf(" %d",tree[i]);
}
return 0;
}
平衡二叉树(AVL)
仍然是查找二叉树(BST),但是需要任意节点的左子树与右子树之差的绝对值不超过1。
其中,左子树 - 右子树 = 平衡因子,也就是说平衡因子的绝对值不能大于1。
struct node{
int val,height; //heigt 表示,以当前节点为根节点的子树的高度
node *left,*right;
};
平衡二叉树主要是对height的情况来构造,所以涉及height的设定就十分关键,默认是root的height最大,叶子位1,新建节点情况如下:
node* newNode(int v){ //v是要插入的值
node* Node = new node;
Node->height = 1;
Node->val = 1;
Node->left = NULL; Node->right = NULL;
return Node;//返回该指针的地址,因为insert使用&,之后直接用root来等于即可。
}
由于返回节点时会存在该指针位NULL的情况,避免报错需要写一个返回高度的函数:
int getHeight(node *root){
if (root == NULL) {
return 0;
}
return root->height;
}
每次插入之后都需要立马更新高度:
void updateHeight(node* root){
root->height = max(getHeight(root->left), getHeight(root->right))+1;
}
处理的情况就是两种,左旋与右旋:
//左旋
void L(node* &root){
node* temp = root->right;
root->right = temp->left;
temp->left = root;
updateHeight(root);//更新节点A高度
updateHeight(temp);//更新节点B高度
root = temp;
}
//右旋
void R(node* &root){
node* temp = root->left;
root->left = temp->right;
temp->right = root;
updateHeight(root);//更新节点A高度
updateHeight(temp);//更新节点B高度
root = temp;
}
与BST的区别在于对以下四种情况的处理:
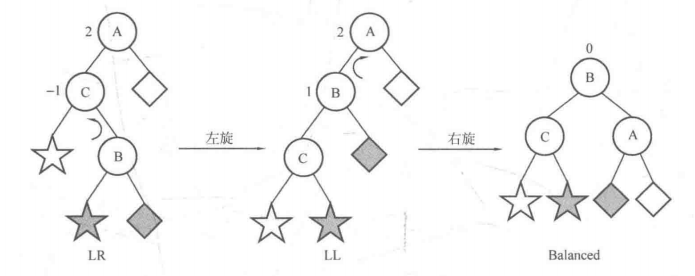
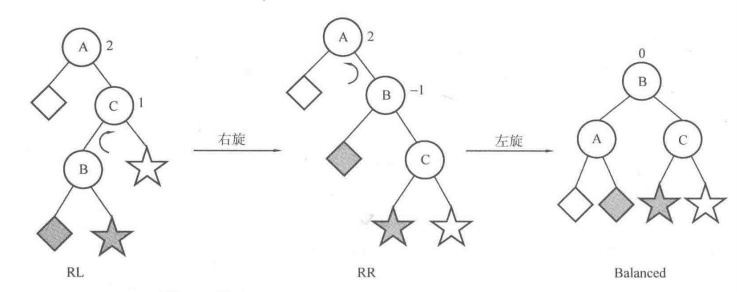

//AVL 的插入代码
void insert(node* &root, int v){
if(root == NULL){
root = newNode(x);
return;
}
if(root->val > v){
insert(root->left,v);
updateHeight(root);
if(getBalance(root) == 2){
if(getBalance(root->left) == 1){
R(root);
}
else if(getBalance(root->left) == -1){
L(root->left);
R(root);
}
}
}else{
insert(root->right,v);
updateHeight(root);
if(getBalance(root) == -2){
if(getBalance(root->right) == -1){
L(root);
}
else if(getBalance(root->right) == 1){
R(root->right);
L(root);
}
}
}
}
并查集
并查集是一种维护集合的数据结构,其实就是个到处认爹的过程,是一个集合的东西就让其中一个认另一个当爹。并查集的每一个集合都是一棵树,可以完成查找、合并的操作。
定义:
int father[N]; //根节点的father是本身
初始化:
for (int i = 0; i < n; ++i)
{
father[i] = i;
}
查找操作:
//找爹
int find(int x){
while(x!=father[x])
x = father[x]
return x;
}
合并:
//首先要确定即将合并的两个元素是否是一棵树上的元素
//查找后若根节点相同则不合并
void Union(int x,int y){
int a = find(x);
int b = find(y);
if(a == b) break;
else{
father[a] = b;
}
}
常涉及有多少个集合的问题,通常解决思路如下:
bool isRoot[N]; //用来存放是否作为根节点。
//在初始化时要全部置false;
//后来对每个找爹,找到的爹都置为true;
哈夫曼树
求解:已知n个数,寻找一棵树,使得树的所有叶子结点的权值恰好为这n个树,并且使得这棵树的带权路径长度最小。(最小生成树问题)
伪代码:
1.初始状态有n个结点,将其视为n棵只有一个结点的树。
2.合并其中根节点最小的两棵树,生成两棵树根节点的父节点,权值为这两个根节点之和,同时减少了一个树的数量。
3.重复2,直到只剩下一棵树为止,这棵树就是哈夫曼树。
很多实际应用场景都不需要真的取构建一棵哈夫曼树,只需要得到最终的带权路径长度,由此可以使用优先队列来执行这种策略,这里插入学习一下stl中的优先队列(priority_queue)的学习。
priority_queue优先队列
队首元素一定是当前队列中优先级最高的那一个。
1.定义:
priority_queue<typename> name;
2.访问:
没有front()与back()函数,只能通过top()函数来访问队首元素。
cout<<q.pop()<<endl;
3.常用函数解析:
q.push();//入队
q.top();//返回队首元素
q.pop();//队首元素出队
q.empty();
q.size();
对基本数据类型来说,优先级根据大小来自动设置,数字越大优先级越高。 非基本数据类定义方式如下:
priority_queue<typename> name;
另一种修改式的优先队列定义:
priority_queue<int, vector<int>, less<int>> name;
//第二个参数类型与第一个参数保持一致。
//第三个参数less表示数字越大优先级越大,若想修改为数字越小优先级越大可以改为:
priority_queue<int ,vector<int>, greater<int>>q;
六、动态规划
动态规划与分治:
虽然都是采用划分成子问题的形式去求解,最后合并,但是分治的子问题是不重叠的,而动态规划的问题是含有重叠子问题的。
动态规划与贪心:
都是要求愿问题必须有最优子结构(一个问题的最优解可以由其子问题的最优解有效地构造出来,那么称这个问题拥有最优子结构),贪心法是从上至下“壮士断腕类”的求解,没有选择的子问题直接抛弃,这样的做法显然不一定能得到最优解。而动态规划需要从边界开始考虑所有子问题的最优情况最后得到最优解,类似于笑到最后才笑的最好。
PAT1033题目让以最小代价到达目的地,存在对线性路径选择加油站的问题,其实是使用贪心来做,我一直误想成了动态规划,但是其实完全可以根据前面的是不是比自己小来决定走不走,所以是不需要解决所有子问题的。
最大连续子序列和
题目类型:给定一个数字序列,求这个数字序列的最大和
如: -2,11,-4,13,-5,-2的最大和是 11-4+13 = 20
设计思路:
使用dp[]数组记录从当前节点开始,包含该节点的最大连续子序列和是多少,递推过程为正即可。
//动态规划过程
dp[0] = a[0];
int ans = dp[0];
for (int i = 1 ; i < n; i++) {
dp[i] = dp[i-1] > 0?(dp[i-1]+a[i]):a[i];
if(ans < dp[i])
ans = dp[i];
}
动态规划可以设计出很多种dp,但必须设计一个拥有午后小的状态以及状态转移方程。
如何设计状态和状态转移方程才是动态规划最难的地方。
最长不下降子序列
题目类型:在一个数字序列中,找到一个最长的子序列(可以不连续),使得这个子序列是非递减的。
如:1,2,3,-1,-2,7,9的最长不下降子序列是{1,2,3,7,9};
设计思路:
使用dp[]数组记录从当前节点开始,包含该节点的最长不下降子序列。递推过程需要对前面所有数进行遍历,并且确保dp是在变大。
//动态规划过程
int ans = 1;
for (int i=0; i<n; i++) {
dp[i] = 1;
for (int j=0; j<i; j++) {
if (a[i] >= a[j] && (dp[j] + 1 > dp[i])) {
dp[i] = dp[j]+1;
}
}
ans = max(ans,dp[i]);
}
两个串的最长公共子序列(LCS)
题目类型:求sadstory 与 adminsorry 的最长公共子序列为adsory,长度为6.
之前的动态规划问题都是比较明显的,这里遇到一个十分经典但是第一次做一脸懵的DP题目,那就是求两个串的最长公共子序列。需要使用到二维dp数组。
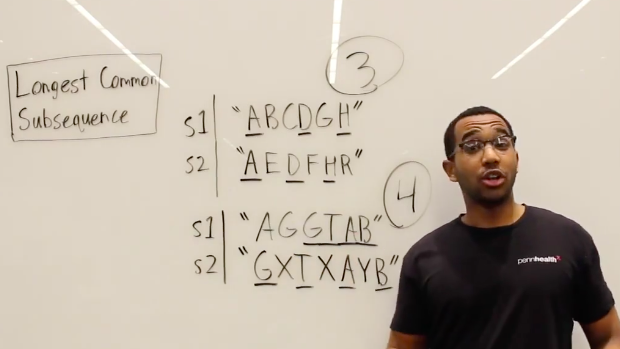
接下来对dp打表,结合代码如下:
打表过程如下:

实现代码如下:
#include <iostream>
#include <cstring>
using namespace std;
int dp[20][20];
int main(int argc, const char * argv[]) {
string a,b;
cin>>a>>b;
memset(dp, 0, sizeof(dp));
for(int i=1;i<=a.size();i++)
for(int j=1;j<=b.size();j++){
if(a[i-1] == b[j-1]){
dp[i][j] = 1+dp[i-1][j-1];
}
else{
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
cout<<dp[a.size()][b.size()]<<endl;
return 0;
}
最长回文子串
题目类型:给出一个字符串如PATZJUJTACCBCC的最长回文串为ATZJUJTA,长度为9.
这是一个二维问题,需要设置二维数组来解决,i代表头,j代表尾,dpij表示i-j的回文子串长度。
动态规划两要素:
1.状态转移方程:
若i,j位置的元素不等,那dpij必为0。若dpij相等,则dpij就等于dp(i-1)(j-1)+2;
2.边界:
dpii = 1,dpii+1一样为1,不一样为0.(相当于先确定长度为1和2的dp值)。
还需注意在枚举时可能出现的问题,因为一般是需要从边界开始枚举这样才能有前一项的内容完成枚举,因此选择将子串的长度从3到目标字符串长度进行处理。
代码实现如下:
dp[i][j];
//dp[i][j] 表示:s[i]至s[j]是回文子串。 其实是为bool类型的,
//最长长度其实是通过便利的最长长度纪录来得到。
ans = 1;
memset(dp,0,sizeof(dp));
//边界
for (int i = 0; i < s.size(); ++i)
{
dp[i][i] = 1;
if(i < len - 1){
if(S[i] == S[i+1]){
dp[i][i+1] = 1;
ans = 2;
}
}
}
//状态转移方程
for(int L = 3;L <= s.size(); L++){ //枚举子串长度
for(int i=0;i+L-1 < s.size();i++){
int j = i + L - 1;
if(S[i] == S[j] && dp[i+1][j-1] == 1){
//dp是i+1,j-1这样才是往里面缩
dp[i][j] = 1;
ans = L;
}
}
}
背包问题
01背包
问题类型:有n件物品,每件物品的重量为w[i],价值为c[i]。现又一个容量为V的背包,问如何选取物品放入背包,使得背包内物品的总价值最大。每件物品只有1件。
//令dp[i][v] 表示前i件物品恰好装入容量为v的背包中所能获得的最大价值。
//状态转移方程
dp[i][v] = max{dp[i-1][v],dp[i-1][v-w[i]]+c[i]}
//首先要确定边界dp[0][v] = 0(0<= v <=V);
//每个状态只与前一个状态有关,因此可以写出代码
for (int i = 1; i <= n; ++i)
{
for (int v = w[i] ; v <= V; v++) //v从w[i]开始考虑
{
dp[i][v] = max(dp[i-1][v],dp[i-1][v-w[i]]+c[i]);
//1.不放第i件物品问题转化为钱i-1件物品恰好装入容量为v的背包中所能获得的最大价值。
//2.放第i件物品,那么问题转化为前i-1件物品恰好装入容量为v-w[i]
}
}
最后在dp二维数组中找最大即可。
01背包状态记录
今天做pat1066的找硬币题目,让从指定的硬币中找出最小可以得到的序列,一开始我竟然完全没反应过来这是01背包问题的板子,因为题目中要求最后的和是确定的,但是要的是最小的硬币数量,是一种变形的01背包问题,因为硬币的价值和原01背包问题的空间量v是对应的,也就是说硬币的价值和空间量相等。
在确定01背包的模板并且可以列出递推式后,还有一个要问题在于我怎么记录得到选了哪些硬币。之前的01背包问题我们都是只得到结果,最优情况的结果,但是若要询问选择过程我还确实有点懵,这也是对算法不熟练导致的。
根据dp填表的规律,此时不仅是一个max可以确定dpij的,因为要知道dpij从何而来,由于越小越好,类似于我们生活中花掉零钱越多越好,我们对已有的硬币降序排序,相当于从最大面额开始往后填,当二维数组中出现可以组合的情况就使用一个bool类型的二维数组进行记录(也就是表现为比较运算符中包含等于)。
在bool型的标记二维数组中寻找时,二维数组也是从后往前遍历,这样就相当于看有没有用到1,用到了的话总值减去1,再看看有没有用到2…依次类推,直到总值减为0.
不得不说这个题的做法实在太巧妙了,再写一遍代码如下:
#include<iostream>
#include<algorithm>
#include<vector>
const int maxn = 100010;
int n,m;
int a[maxn];
bool has[maxn][110] = {false};
int dp[maxn][110] = {0};
//取前i个数,在能取的价值小于等于m的情况下能屈能取的最大价值。
bool cmp(int a,int b){
return a > b;
}
int main(){
scanf("%d %d",&n,&m);
for (int i = 1; i <= n; ++i)
{
scanf("%d",&a[i]);
}
sort(a+1,a+1+n,cmp);
for (int i = 1; i <= n; i++)
{
//边界设定
dp[0][i] = 0;
}
for (int i = 1; i <= n; i++)
{
for (int j = a[i]; j <= m; j++)
{
int sum = dp[i-1][j-a[i]]+a[i];
if (sum >= dp[i-1][j])
{
dp[i][j] = sum;
has[i][j] = true;
}
else{
dp[i][j] = dp[i-1][j];
}
}
}
if (dp[n][m] == m)
{
while(m){
vector<int> v;
while(!has[n][m]){
n--;
}
v.push_back(n);
m -= a[n];
}
for (int i = 0; i < v.size()-1; i++)
{
cout<<v[i]<<" ";
}
cout<<v[v.size()-1]<<endl;
}
else
printf("No Solution\n");
return 0;
}
完全背包
问题类型:有n件物品,每件物品的重量为w[i],价值为c[i]。现又一个容量为V的背包,问如何选取物品放入背包,使得背包内物品的总价值最大。每件物品都有无穷件。
唯一的区别在于max的第二项,是转移到i项而不是i-1。