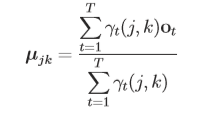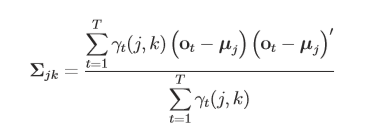隐形马尔可夫模型，英文是 Hidden Markov Models，所以以下就简称 HMM。 既是马尔可夫模型，就一定存在马尔可夫链，该马尔可夫链服从马尔可夫性质：即无记忆性。也就是说，这一时刻的状态，受且只受前一时刻的影响，而不受更往前时刻的状态的影响。

先来看一个类似例子：

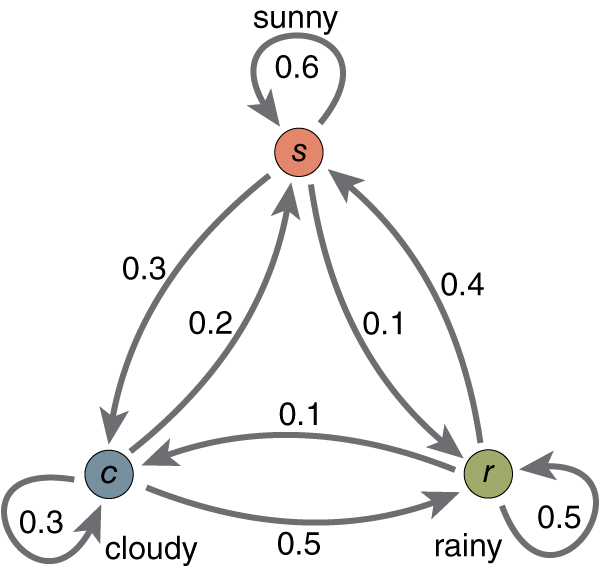
在这个马尔可夫模型中，存在三个状态，Sunny， Rainy， Cloudy，同时图片上标的是各个状态间的转移概率（图中箭头的权）。

这里我们主要先来了解一下其中的Elements。

1.N(Number of states N)

这里的N表示状态数，放在上述例子就是Sunny， Rainy， Cloudy，而这些状态是隐式的、不可观测的（我们可以假想一个犯人在没有窗户的监狱里，他只能根据守卫的穿着猜测天气）。同时规定：t时刻的状态是qt。

2.M(Model parameter M)

模型参数M是我们观测序列的数量，由上例子：

如果规定

Sunny ————> 守卫穿短袖的概率大
Rainy ————> 守卫带伞的概率大
Cloudy————> 守卫穿棉衣的概率大

那么犯人所观测的守卫穿短袖、守卫带伞、守卫穿棉衣数量就是M。

3.π (Initial state distribution π)

初始状态分布 π ，即我们考虑状态转移前最初的状态，也就是以上例子中的第一天会是什么天气。

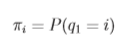
4.A (State transition probability distribution)

表示状态的转移可能分布。

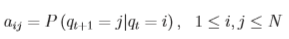
表示t时刻状态为i，在t+1时刻状态为j的概率，也就是上例中比如第一天下雨第二天会是晴天的概率。

5.B (Observation symbol probability distribution)

表示可观测信号可能分布。

λ=(A,B,π)

λ 知道则代表三个概率知道，λ 用于构造出模型。

模型λ由三个对象确定表示：λ=(A, B, π)=(状态转移概率分布，观测概率分布，初始状态概率分布)

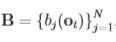
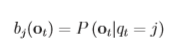
有了基础的认识结合实际例子来理解三个问题会好一点： 现在假设我异地恋要根据女友的行为猜测天气： 在这里，为了简化，把天气情况简单归结为晴天和雨天两种情况。雨天，她选择去散步，购物，收拾的概率分别是0.1，0.4，0.5， 而如果是晴天，她选择去散步，购物，收拾的概率分别是0.6，0.3，0.1。而天气的转换情况如下：这一天下雨，则下一天依然下雨的概率是0.7，而转换成晴天的概率是0.3；这一天是晴天，则下一天依然是晴天的概率是0.6，而转换成雨天的概率是0.4. 同时还存在一个初始概率，也就是第一天下雨的概率是0.6， 晴天的概率是0.4.

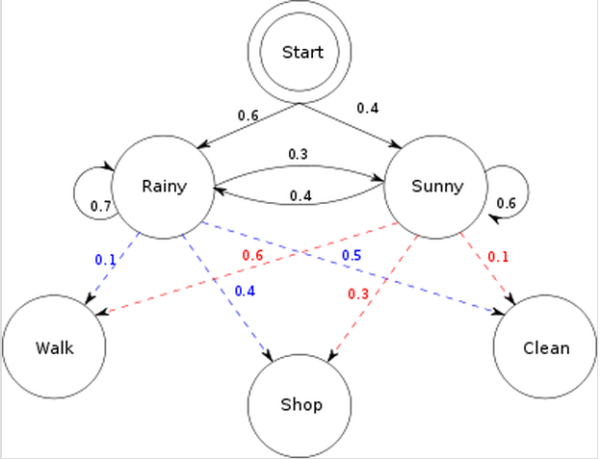
根据以上的信息，我们得到了 HMM的一些基本要素：初始概率分布 π，状态转移矩阵 A，观测量的概率分布 B，同时有两个状态，三种可能的观测值。

现在，重点是要了解并解决HMM 的三个问题。

• 问题1，已知整个模型，我女朋友告诉我，连续三天，她下班后做的事情分别是：散步，购物，收拾。那么，根据模型，计算产生这些行为的概率是多少。

• 问题2，同样知晓这个模型，同样是这三件事，我女朋友要我猜，这三天她下班后北京的天气是怎么样的。这三天怎么样的天气才最有可能让她做这样的事情。

• 问题3，最复杂的，我女朋友只告诉我这三天她分别做了这三件事，而其他什么信息我都没有。她要我建立一个模型，晴雨转换概率，第一天天气情况的概率分布，根据天气情况她选择做某事的概率分布。

总结隐马尔可夫模型有3个问题：概率计算问题、学习问题、预测问题

Three Basic Problems

Solution to Problem 1

The Forward Algorithm

概率计算问题描述如下：

已知一个隐马尔可夫模型λ=（A，B，λ），已知一个观测序列O=（o1, o2,……，oT）

问题：请计算在模型λ下观测序列O出现的概率P(O| λ)

前向概率如下： 已知隐马尔可夫模型λ=（A, B, π），定义到时刻t(t<T)，观测序列为o1, o2, ……，ot，状态为qi的概率为前向概率，记作：

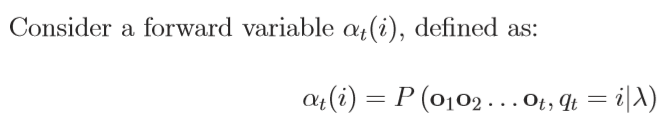
可以递推得前向概率以及观测序列概率P(O|λ)： 输入：隐马尔卡夫模型λ=(A, B, π)，观测序列O 输出：观测序列概率P(O | λ)

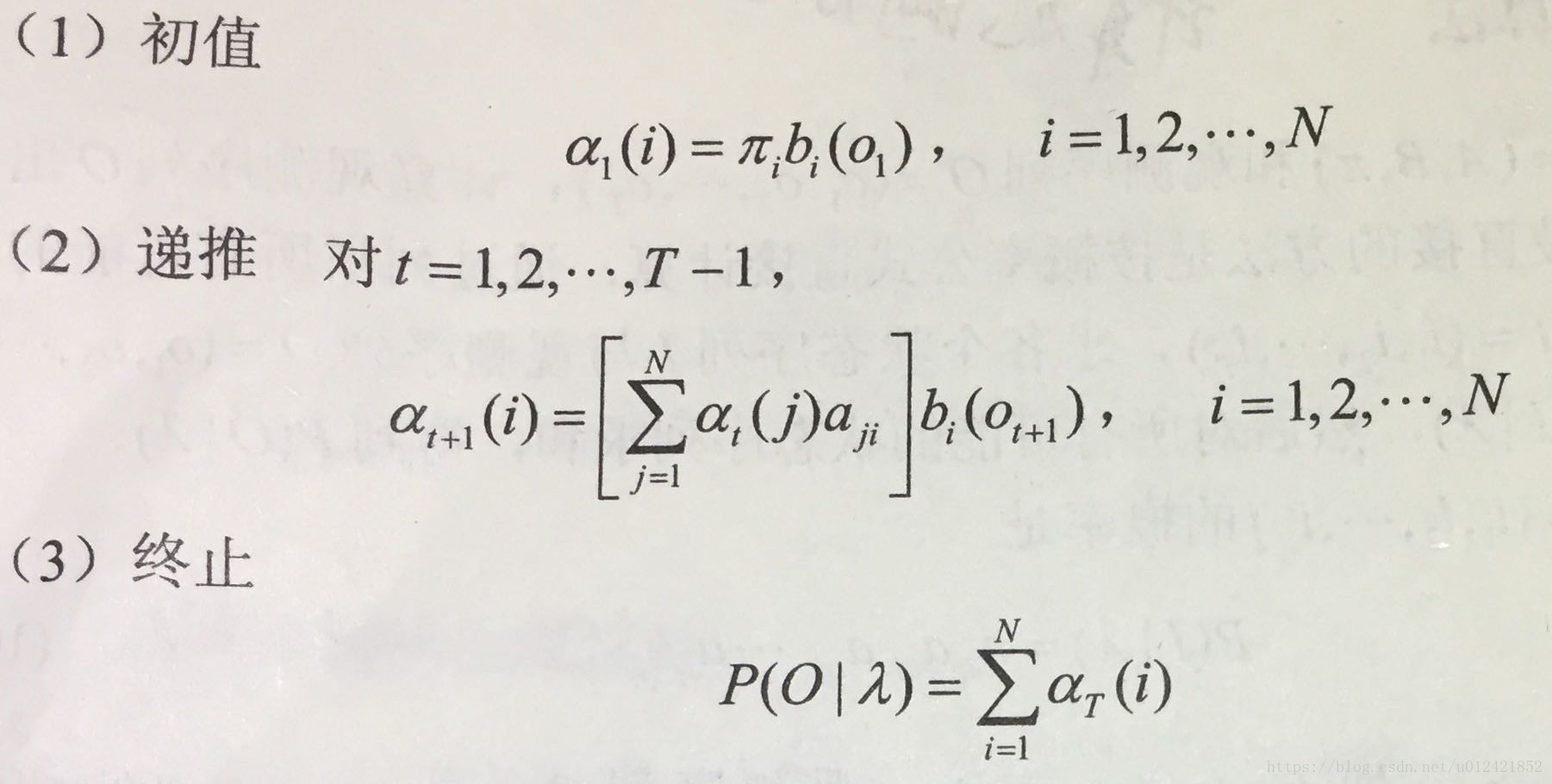
有关第一个问题的解决可以使用向前算法。

先计算 t=1时刻，发生『散步』一行为的概率，如果下雨，则为 P(散步，下雨)=P（第一天下雨）X P（散步 | 下雨）=0.6X0.1=0.06；晴天，P（散步，晴天）=0.4X0.6=0.24

接下来完成地推计算：

t=2 时刻，发生『购物』的概率，当然，这个概率可以从 t=1 时刻计算而来。

如果t=2下雨，则 P（第一天散步，第二天购物， 第二天下雨）= 【P（第一天散步，第一天下雨）X P（第二天下雨 | 第一天下雨）+P（第一天散步，第一天晴天）X P(第二天下雨 | 第一天晴天)】X P（第二天购物 | 第二天下雨）=【0.06X0.7+0.24X0.3】X0.4=0.0552

如果 t=2晴天，则 P（第一天散步，第二天购物，第二天晴天）=0.0486 （同理可得，请自行推理）

如果 t=3，下雨，则 P（第一天散步，第二天购物，第三天收拾，第三天下雨）=【P（第一天散步，第二天购物，第二天下雨）X P（第三天下雨 | 第二天下雨）+ P（第一天散步，第二天购物，第二天天晴）X P（第三天下雨 | 第二天天晴）】X P（第三天收拾 | 第三天下雨）=【0.0552X0.7+0.0486X0.4】X0.5= 0.02904

如果t=3，晴天，则 P（第一天散步，第二天购物，第三天收拾，第三天晴天）= 0.004572

那么 P（第一天散步，第二天购物，第三天收拾），这一概率则是第三天，下雨和晴天两种情况的概率和。0.02904+0.004572=0.033612.

引用摘自：https://www.zhihu.com/question/20962240/answer/64187492

The Backward Algorithm

后向算法与前向算法大致相同，已知隐马尔可夫模型λ=（A, B, π），定义到时刻t(t<T)状态为q<i>的条件下，从t+1到T的部分观测序列为o<t+1>,o<t+2>，…,O的概率为后向概率，记作：

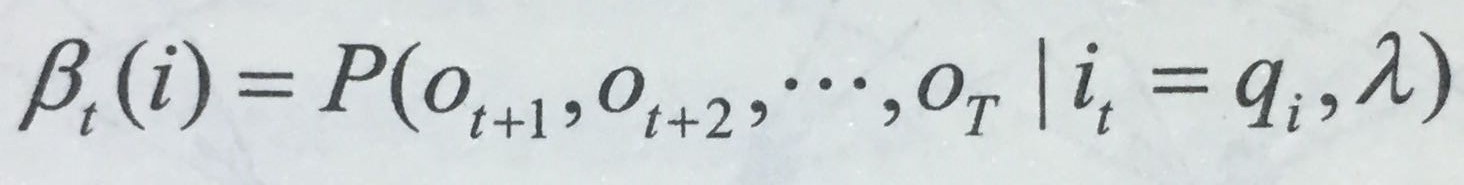
（这里简单归纳一下：前向算法考虑的是o1,o2,…ot的观测序列，而后向算法考虑的是ot+1,…oT的观测序列）

可以递推得后向概率以及观测序列概率P(O | λ) 输入：隐马尔卡夫模型λ=(A, B, π)，观测序列O 输出：观测序列概率P(O | λ)

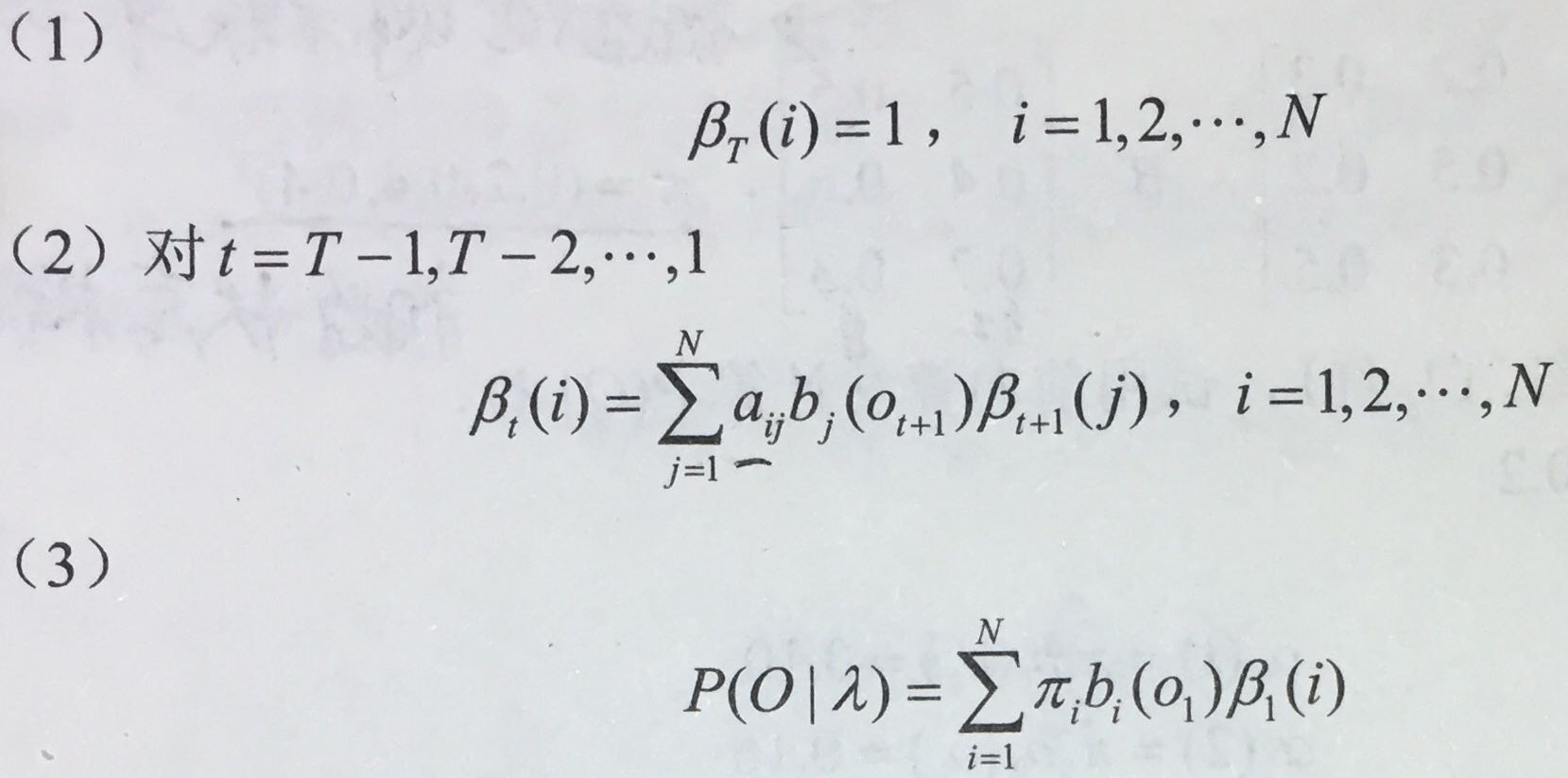
（首先是定义β在T时刻的概率是确定的所以为1）

那么，如何具体实现计算呢： 以前向算法的条件为例子。

首先根据初始化条件（Initialization）我们得知，此时在下雨/晴天的情况下『打扫房间』的概率都是1。 即P（打扫|第三天下雨）=1，P（打扫|第三天晴天）=1

接下来完成地推计算

t=3时刻，考虑前一个状态是下雨，则 P（前一个状态是下雨，第三天打扫房间）= p（前一个状态下雨现在还是下雨）*（下雨的时候打扫房间）* P（打扫|第三天下雨） + p（前一个状态下雨现在是晴天）*（晴天的时候打扫房间）* P（打扫|第三天晴天）= x31

同样是t=3时刻，考虑前一个状态是晴天，则 P（前一个状态是晴天，第三天打扫房间）= p（前一个状态晴天现在是下雨）*（下雨的时候打扫房间）* P（打扫|第三天下雨） + p（前一个状态下雨现在是晴天）*（晴天的时候打扫房间）* P（打扫|第三天晴天）= x32

这时候就求出了 t=3 下雨、晴天状态的后向概率，即x31，x32

下面用时刻3的后向概率 递推计算 时刻2的后向概率：

t=2时刻，考虑前一个状态是下雨，则 P（前一个状态是下雨，第二天购物,前前一个状态是下雨，第三天打扫房间）= p（前一个状态下雨现在还是下雨）*（下雨的时候购物）* x31 + p（前一个状态下雨现在是晴天）*（晴天的时候购物）* x32 = x21

同样是t=3时刻，考虑前一个状态是晴天，则 P（前一个状态是晴天，第三天打扫房间）= p（前一个状态晴天现在是下雨）*（下雨的时候购物）* x31 + p（前一个状态下雨现在是晴天）*（晴天的时候购物）* x32= x22

这时候就求出了 t=2 下雨、晴天状态的后向概率，即x21，x22

终止,t=1 t=1时刻计算与递推时大同小异, 只是把转移概率换成初始概率,求得x11,x12,x13。

则这个后向概率就是 sum(x11+x12+x13)。

核心是通过模型λ=(A, B, π)以及时刻t+1的β<t+1>(i)来递推得到前一个时刻t的β<t>(i).直到递推得到β<0>(i)

那么前向后向算法有何联系呢？

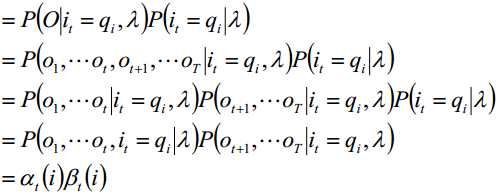
不难看出，在t时刻如果知道了状态为qi，那么可以将这个t之前和之后阻断，最后变换成前向概率和后向概率，这样我们就可以求单个概率了。这个性质在问题三预测模型时对我们有极大帮助。

Scaling the Forward and Backward Variables

概率之间会出现越乘越小的问题，若最后不能被计算机所识别则前面一切的累计都是徒劳的，所以进行归一化处理十分有必要，具体推导如下：

1.首先进行归一化处理：

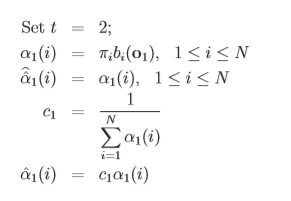
2.归纳为如下情况：

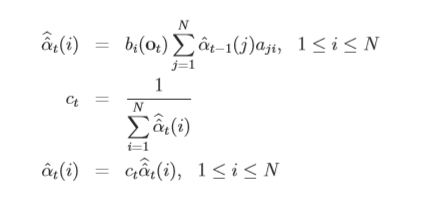
3.可由前向公式的Termination取对数化简后为：

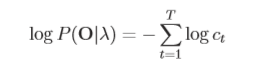
Solution to Problem 2

为解决第二个问题我们引入维特比算法（Viterbi Algorithm），其目标是找到单个最优状态序列。在学习时感觉维特比算法格外亲切，其实际是用动态规划解隐马尔可夫模型预测问题，就是用动态规划(dynamic programming)求概率最大路径（最优路径）。 这时一条路径对应着一个状态序列。类似有向图(转移概率为权重)找最优路径，即与上个学期在数据结构中所学的迪杰斯特拉算法类似。

算法详解： 首先导入两个变量δ(delta)和ψ(psi) 1.在时刻t状态为i的所有单个路径(i1, i2, …, it)中概率最大值δ[t, i]

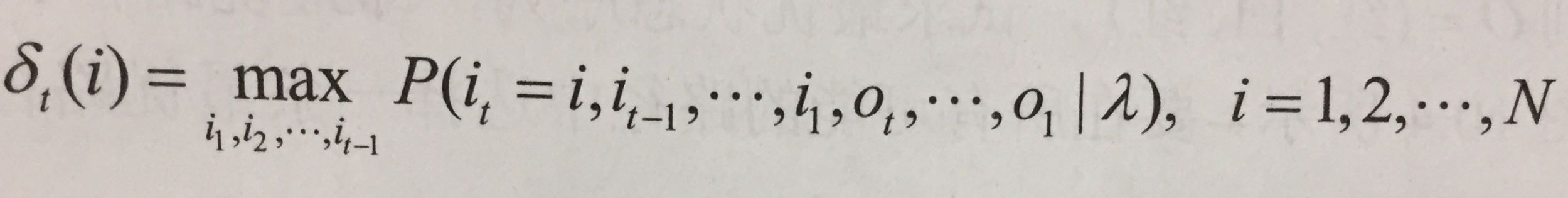
（δ表示概率）

2.变量δ的递推公式

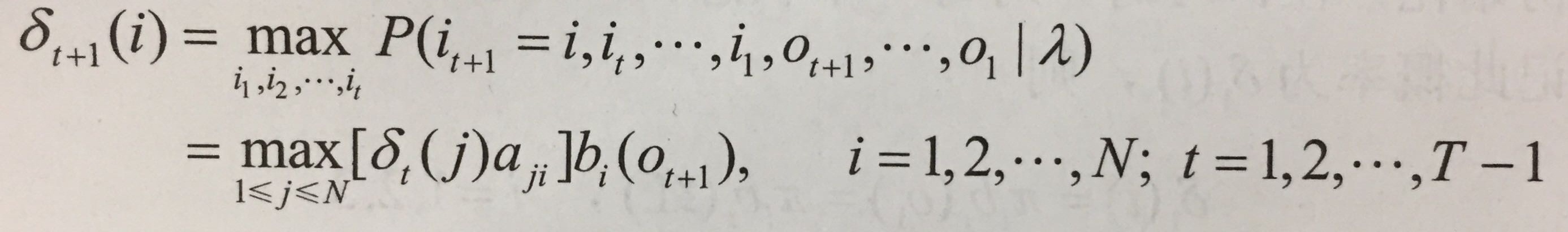
这里就是考虑δt的情况、以及从状态j到i的转移的最优情况，最后尾巴×一个发射概率。

3.在时刻t状态为i的所有单个路径(i1, t2,…,it-1,i)中概率最大的路径的第t-1个节点

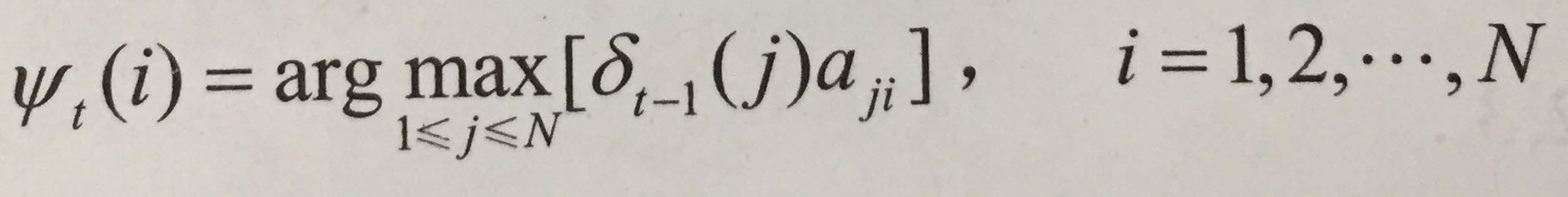
（ψ相当于第t-1时刻状态）

4.下面介绍维特比算法

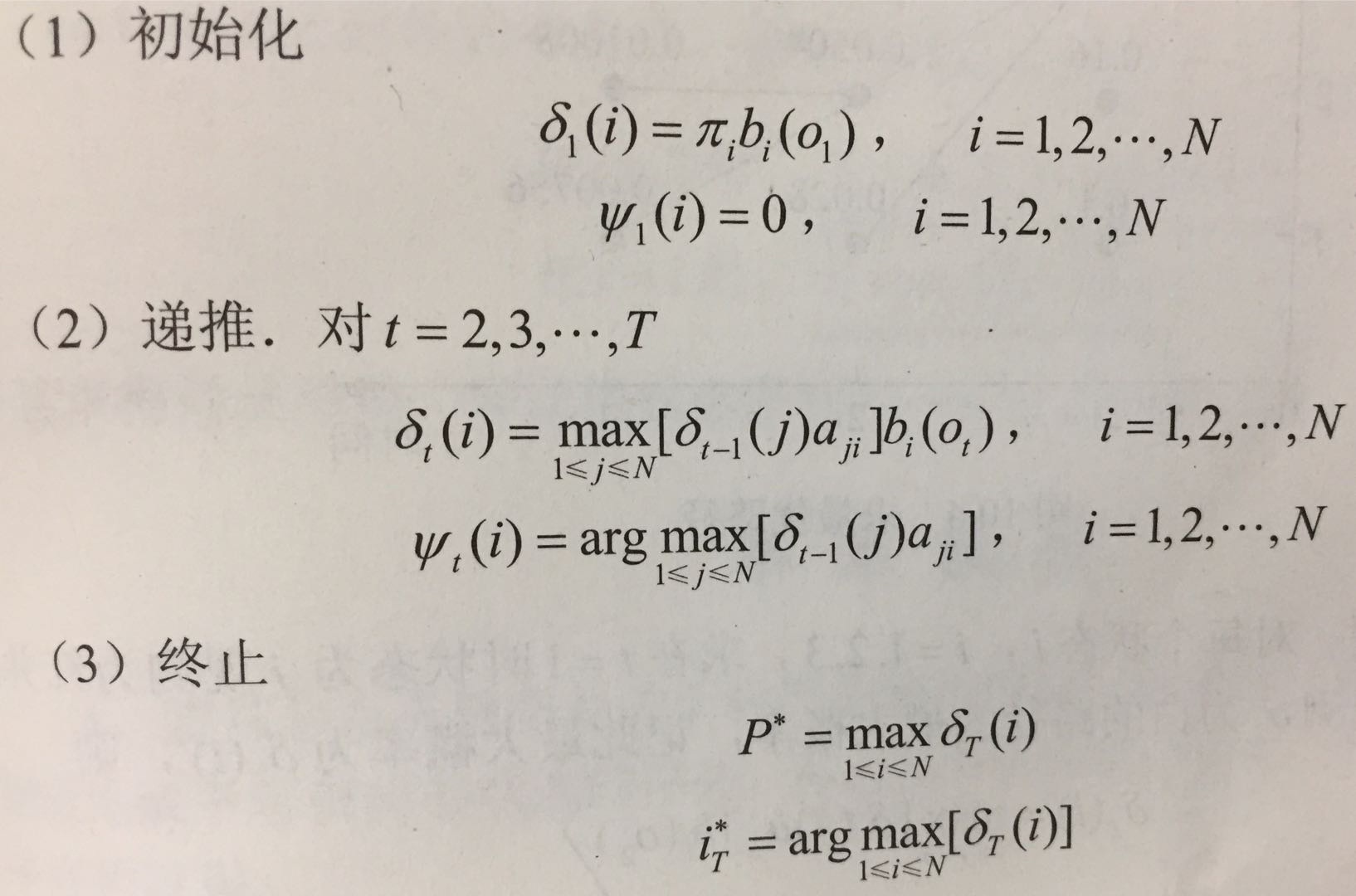
（arg max表示当后面取最大值时，自变量的取值） （此时ψ）

5.最后一步，就是最优路径回溯

这里小结一下，与迪杰斯特拉求最短路径相比较，这里其实就是把路径最短问题类比为概率最大问题，

Solution to Problem 3

第三是让我们估计模型的变量，即λ（A,B,π），可以表达为公式：

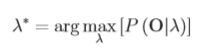
问题三是三个问题中最难解决的，因为没有一个已知的方法仅仅根据观测序列去分析找到概率最大的模型变量，但要使得模型变量有最大的可能性一般采用Baum-Welch方法（也叫期望最大化方法）或者梯度法。

考虑到以下三个点，我们采用期望最大化的方法，

• Baum-Welch在数值上是稳定的，并且每一次迭代的可能性都不会减少。

• Baum-Welch收敛到一个局部最优。

• Baum-Welch具有线性收敛性。

A,B,π 逐个考虑，首先考虑转移概率：

定义如下ξ为在t时刻状态是i，t+1时刻状态是j，在给定 λ 、O的条件下的概率：

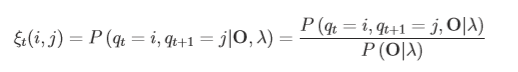
ps：第二个式子到第三个式子经过了条件概率的变换。

接下来就用到了前面说的前向算法和后向算法的利用，转换为：

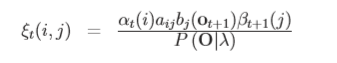
分母考虑全概率公式得到：

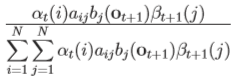
这时我们考虑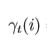,γ定义为在t时刻状态为i的可能性，即：

考虑其与ξ的关系为：

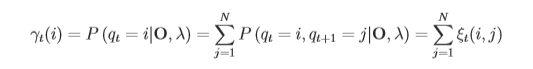
这时我们思考，γt(i)既然能表示t时间i状态，那全时间的量被我们利用起来能得到什么？

第一行表示出了状态i的初始概率 第二行表示出了从状态i转移的概率 第三行表示出了从状态i转移到状态j的概率

鉴于此，π的公式可以推导如下：

A的公式如下：

(其实这里给我的感觉是还是要靠全面的语料才能给出)

B的推断相对要复杂一些，因为是发射概率，直接决定着我们的观测序列是什么，所以为了保证准确性我们需要有各个方面的考量，这就引入了多维高斯分布。

这里我们可以具体想象以下，结合一个属性我们得到一个属性的峰值可能是我们想要的，但语音识别领域真正把语音转化成文字就得需要各个方面的敲定，就像是一要找到一个立体的图的峰值点。

由此我们引入一个cjk，cjk是在状态j使用到k这个混合分类与在j这个状态总的比值，这个混合分量可以理解为，k有没有为这个值的得出做出贡献，有一种赋予了0或1权值的感觉。

接下来就是介绍一下µjk、 Σjk 的求法：